Calcule a fem e a fem no circuito abaixo e a diferença de potencial do ponto em relação ao ponto .
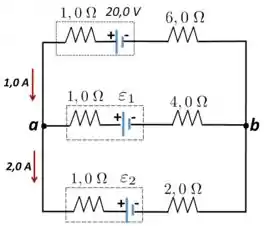
Passo 1
A gente tem dois valores de correntes, cujos sentidos já foram informados, em vermelho, na Figura. Então, olhando para o ponto do circuito, chega a corrente de e sai uma outra corrente de valor .
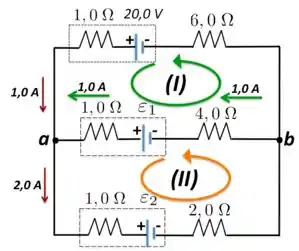
Se usamos a lei dos nóis em , então chega uma corrente de que, somada à outra de , resulta em uma de . Além disso, essa corrente em verde flui de para . Tranquilo?
Passo 2
Agora, vamos olhar para a malha em verde na Figura acima. Partindo do ponto e percorrendo essa malha em verde no sentido anti-horário e voltando para o ponto , temos, aplicando a lei das malhas:
em que indicamos as unidades para facilitar que você veja cada elemento do circuito nessa malha . Reforçando, começamos do ponto e voltamos ao ponto , por isso, depois de uma volta completa, temos zero, blz?
Dessa expressão, a gente consegue tirar o valor da fem , que é:
Passo 3
Para calcular o valor da outra fem , utilizamos a outra malha indicada na cor laranha na Figura acima, que está no sentido anti-horário. De novo, partindo do ponto e voltando para o ponto , teremos:
Como , teremos que
Passo 4
Para fechar, vamos tomar o trecho do circuito de para apenas. Se o potencial do ponto é e o de é , então:
Portanto, a diferença de potencial de em relação a é dada por