Fundamentos de Fisica - Vol. 3. Halliday - 9ª Edição, Capítulo 27 – seção 7 - Problema 29.
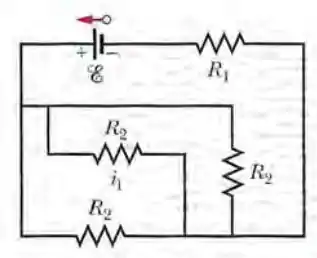
(Cap 27 Ex – 29) Na Fig. 27-40,, e a força eletromotriz da fonte ideal é . Determine (a) o valor absoluto e (b) o sentido (para a esquerda ou para a direita) da corrente . (c) Qual é a energia total dissipada nos quatro resistores em 1,00 min?
Passo 1
Falaaa galerildes !! Como vocês estão no dia de hoje?
Espero que bem e animados !!
Vocês concordam comigo que este desenho está dificultando nossa life? Pois é ! Vamos redesenhar, mas antes reparem que as resistências 2 estão em paralelo:
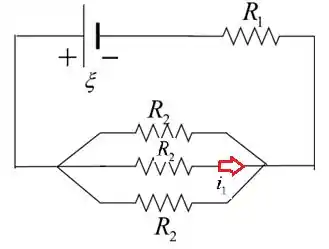
Se os resistores 2 estão em paralelos a resistência equivalente pode ser dada por:
Lembrando que:
Então:
Esta nova resistência está em série com a resistência 1, certo? E neste caso a resistência equivalente é dada pela:
Mas em que esta resistência nos ajuda?
Passo 2
Com ela a gente acha fácil a corrente, basta você lembrar da fórmula:
Lembrando que:
Então:
Chegamos ao resultado?
Que nada !! Nós queremos a corrente que passa pelo resistor 2, que o problema chamou de
Como temos a corrente se dividindo para três resistores iguais:
Bom, aqui nós acabamos respondendo a letra (a) e (b), não é?
Se é positivo a corrente está na mesma direção que inicialmente foi assumida, ou seja, ela está indo para a direita !!
Tudo bem até aqui?
Passo 3
Na letra (c) nós queremos saber qual é a energia total dissipada nos quatro resistores em 1,00 min.
Bom galerinha, a energia total dissipada pelos quatro resistores pode ser calculada como:
Ficou moleza !! Se nós já temos todos os dados é só substituir:
E finalizamos mais umaa !!
Resposta
- Para a direita