(A)
(B)
(C)
(D)
(E)
Passo 1
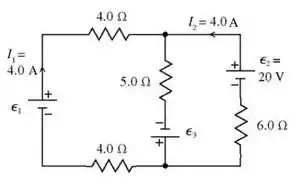
As duas correntes e , as duas de se encontram no resistor de .. Assim, uma corrente de passa na resistência de de cima para baixo. Vamos então olhar para a segunda malha (direita) e percorrer ela no sentido anti-horário:
Com isso já podemos marcar a letra (A). Mas vamos continuar...
Passo 2
Vamos aplicar o mesmo raciocínio para a primeira malha, da esquerda, rodando ela no sentido horário:
Substituindo o que a gente viu no passo anterior:
Resposta
Letra (A).
Exercícios de Livros Relacionados
Verifique seus resultados para o Problema 79 usando os seguintes valores específicos: (a) R1 = 4,00 Ω, R2 = 6,00 Ω; (b) R1 = 4,00 Ω, R3 = 3,00 Ω; e (c) R2 = 6,00 Ω, R3 = 3,00 Ω.
Um comprimento de arame tem uma resistência de 120Ω . O arame é cortado em pedaços que têm o mesmo comprimento, e então os arames são conectados em paralelo. A resistência do arranjo paralelo é de 1,8
(a)Resistência a resistência equivalente entre os pontos a e b na Figura 26-56. (b) Se a queda de potencial entre os pontos a e b é 12V , determine a corrente em cada resistor.
(a)Determine a resistencia equivalente entre os pontos a e b na figura 25.57. (b)Se a queda de potencial entre os pontos a e b é 12V , determine a corrente em cada resistor.
Quatro resistores de 18,0 Ω são ligados em paralelo a uma fonte ideal de 25,0 V. Qual é a corrente na fonte?