Fundamentos de Fisica - Vol. 3. Halliday - 9ª Edição, Capítulo 27 – seção 7 - Problema 33.
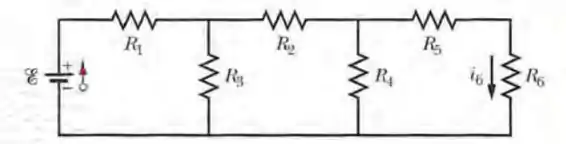
(Cap 27 Ex – 33) Na Fig. 27-44, a corrente na resistência 6 é e as resistências são , , e . Qual é a força eletromotriz da fonte ideal?
Passo 1
Falai galerinha do Responde ai, tudo belezinha?
Bora resolver essa comigo
Nesta questão temos um circuito que tem apenas uma fem porem devemos fazer uma análise das resistências para ver quais estão em paralelo e quais estão em série.
Note que , a queda de tensão em , é a soma das quedas de tensão em e :
Isso significa que a corrente em é dada por
.
De acordo com a regra dos nós, a corrente em é
e, portanto, a queda de tensão em é
Passo 2
De acordo com a regra das malhas, a queda de tensão em é
e, portanto, a corrente em é
Assim, de acordo com a regra dos nós, a corrente em é
o que significa que a queda de tensão em é
e, portanto, de acordo com a regra das malhas,
.
Resposta
a)