Um microscópio de força magnética usa a alta sensibilidade de uma haste micrométrica a variações de força para medir o gradiente de força magnética em uma região.
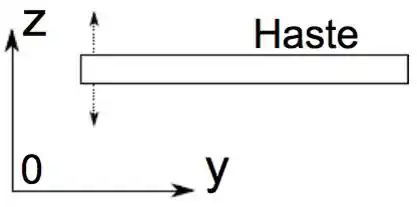
O movimento de oscilação da extremidade da haste se dá na direção perpendicular a haste, como ilustra a figura, e tem uma frequência angular própria . Para simplificar a questão, consideraremos a equação do movimento da extremidade da haste, sem força externa, da seguinte forma: . Um mecanismo permite excitar a haste com uma força de amplitude . A frequência angular é um pouco inferior a frequência angular própria da haste.
- Escreva a equação diferencial de movimento do oscilador harmônico forçado. Considere que é a massa efetiva haste (massa em movimento durante as oscilações).
- Escreva a solução da equação homogênea, a solução particular da equação inomogênea e a solução geral da equação inomogênea.
- Suponha A PARTIR DE AGORA que uma força externa ADICIONAL atua sobre a haste. Como varia a frequência de ressonância se esta força adicional for tipo ?
- Para uma excitação a uma frequência angular inferior a , como varia (qualitativamente) a amplitude com a presença da força ?
Passo 1
a)
A equação vai ser semelhante aquela do oscilador sem a força externa. A forma geral da equação é, com uma força externa ,
Aquela da equação está com a segunda derivada sem a massa para isso vamos dividir essa equação pela massa.
Nessa questão, não temos amortecimento, assim, a equação não vai ter o termo Na do enunciado, o lado esquerdo já foi dado, o lado direito vai ser a força externa divida pela massa
O vetor só indica que é no .
Passo 2
b)
Para a solução da equação homogênea devemos fazer como fazemos para o MHS. A equação auxiliar que fica
Resolvendo a equação de segundo grau vamos achar
Desse jeito temos um amortecimento subcrítico com
achando a seguinte solução da equação homogênea
Passo 3
Lembra de cálculo? Quando temos uma função seno ou cosseno do lado direito da equação inomogênea, considerando solução da particular fica
A primeira e segunda derivada, em relação ao tempo, ficam
Substituindo na equação inomogênea vamos ter
O coeficiente do cosseno e do seno devem ser iguais nos dois lados da equação, resultando no sistema
Da primeira equação vamos ter
e da segunda equação teremos
Então a solução da particular fica
Passo 4
A solução geral da equação fica
Passo 5
c)
Agora a força externa passa a ser
Essa equação é parecida, mas a frequência de ressonância vai ser
Na teoria vimos que basta dividir o que multiplica por pela massa e colocar dentro da raiz, mas nessa forma a divisão pela massa já foi feita, então só precisamos colocar na raiz.
Como é positivo a frequência vai diminuir, já que pela mesma lógica a frequência de ressonância inicial é
Passo 6
d)
A frequência da força é levemente menor que a frequência de ressonância. Colocando a força a frequência de ressonância diminui, o que faz a frequência da força externa se aproximar da ressonância, fazendo assim amplitude aumentar
Resposta
- Diminui
- Aumenta