Um bloco de massa m, que pode deslizar sem atrito sobre um plano inclinado de um ângulo , está conectado ao topo do plano por uma mola ideal, que obedece à lei de Hooke, com constante elástica k e comprimento L quando não deformada.

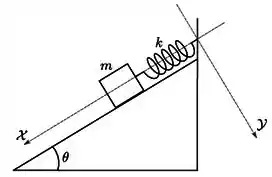
(a) Calcule a distância que o bloco se encontra do topo do plano inclinado na posição de equilíbrio.

(b) Deduza a equação de movimento do sistema, em termos da distância ao topo do plano inclinado.

(c) Resolva a equação de movimento, obtida no item anterior, para o caso do bloco ser solto do repouso a uma distância b, ao longo do eixo X indicado na figura, acima da posição de equilíbrio.

b) Agora nós vamos escrever a mesma coisa que na letra a, só que com força resultante diferente de zero e pra um x qualquer:

E lembrando que:

c) Agora ele pede que a gente resolva essa equação do item b.

Essa equação vai ter uma solução homogênea e uma solução particular.

A solução homogênea é a mesma do MHS:

E como a parte particular deve parecer com o lado direito da equação (constante) vou chutar um valor constante pra ela:

E derivando:

Beleza, agora vamos substituir na EDO:

Então:

Olha que engraçado, vai ser exatamente igual a !

E a solução geral vai ser:

Para descobrir as constantes e vamos usar as condições iniciais:

E pra outra condição inicial:

Como:

O valor de deve ser negativo, porque é positivo e (lembra que ele disse que b tá acima da posição de equilíbrio?). Então:

A solução geral vai ficar:

Com: