Uma pessoa está em pé sobre uma balança de banheiro que está sobre uma plataforma suspensa por uma grande mola. A plataforma executa um movimento harmônico simples vertical. Descreva a variação de leitura da escala da balança durante um período.
Passo 1
Vamos primeiro ver as forças que estão atuando nesse ser humano. Só a força peso e a força elástica, certo?
A força peso tá apontando pra baixo, como de costume, e a força elástica apontando pra cima, sempre contrária ao movimento. Então a força resultante vai ser:
Vamos trocar pelas fórmulas de peso e força elástica. E como força resultante é massa vezes aceleração:
Tá lembrando do que é isso? Essa aí é uma EDO de oscilação forçada com força externa constante e igual à força peso.
Puts, falei grego pra você? Dá uma olhada rápida lá na teoria de Oscilações Forçadas que tudo fica mais claro.

Passo 2
Tá, e como a gente resolve isso? Essa equação vai ter uma solução homogênea, igualzinho à do MHS, e uma solução particular, devido à força externa. Então:
E a solução particular a gente acha chutando uma solução parecida com ela e substituindo na EDO. Como a força externa é constante, a gente chuta que a solução particular também é. Tipo assim:
Depois é só substituir na EDO pra achar o valor de C. Lá na teoria tem o passo a passo bonitinho, mas fazendo essa conta a gente acha que:
Então a nossa solução vai ser:
Passo 3
Beleza! Ele quer a leitura da balança né? E quando eu ou você estamos nos pesando lá na balança da farmácia, a leitura que ela mostra é a massa. Mas nessa leitura a força resultante é igual ao peso, porque não tem essa bobeira de plataforma oscilatória.

Então a balança tá pegando a força resultante e dividindo pela aceleração da gravidade. Porque ela recebe o peso, que é igual a , e retorna só . Tendeu?
Então a leitura da nossa balança vai ser:
Ou seja:
Passo 4
Vamos achar então a leitura da balança. A gente achou que a posição é:
Então a aceleração vai ser, a segunda derivada, igual a:
Show! Então trocando na fórmula que achamos pra leitura da balança:
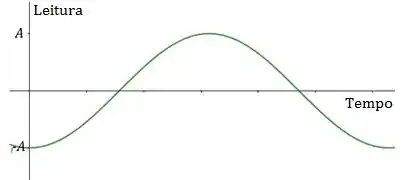
Em que:
Resposta
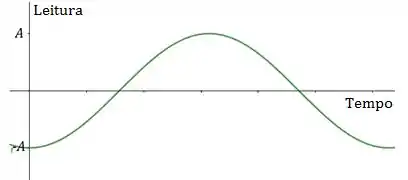
Em que: