No sistema bloco-massa da figura, o bloco possui uma massa de e a mola possui massa desprezível. O sistema está sobre uma superfície sem atrito que faz um ângulo de com a horizontal.
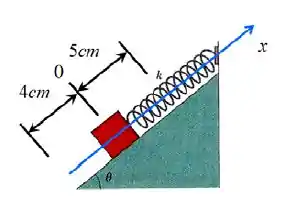
- Sabendo que quando o sistema está em equilíbrio estático a mola sofre uma elongação de , calcule a constante da mola.
- Em seguida, a mola é puxada mais e depois solta em . Encontre a frequência angular e o período .
- Determine a equação de movimento, a velocidade e a aceleração.
Se necessário use e .
Passo 1
a)
Quando o bloco está em equilíbrio, a força da mola equilibra o peso na direção do plano inclinado:
Então:
Passo 2
b)
Ai vem um macete: A frequência angular só depende da constante da mola e da massa do bloco. Logo:
E o período:
Passo 3
c)
Vamos montar a EDO responsável pelo movimento. As forças que agem sobre o bloco são a força peso, no caso a sua componente na direção do plano, e a força elástica. Logo:
O sinal do peso é negativo devido ao eixo que arbitrado na figura. Logo:
Bo resolver isso como a gente aprendeu a resolver uma EDO. Vamos resolver a equação homogênea primeiro:
E equação relacionada será:
Como é complexo, a solução da homogênea será:
E a solução particular será:
Onde é uma constante. Logo:
Logo:
Agora vamos parra as condições de contorno. Vamos considerar como a nossa origem o ponto de equilíbrio do sistema. Então, o deslocamento inicial será Então, para :
:
E como o bloco parte do repouso, Derivando a expressão acima e substituindo os valores:
Logo a solução é:
Então a velocidade será dada por
E a aceleração será dada por
Resposta
a)
b)
c)