Um tubo é cortado em duas partes. Numa das partes, com uma extremidade aberta e outra fechada, a frequência sonora fundamental é de 256 Hz. Na outra parte, com ambas as extremidades abertas, a frequência sonora fundamental é de 440 Hz. A velocidade do som no ar é 343 m/s. Qual é o comprimento original do tubo?
Passo 1
E aí, galerinha! Tudo na paz por aí?
Não se assuste, essa questão é mais tranquila do que você imagina e eu posso te provar hahaha
Bem, a primeira coisa é pensar em como a gente vai conseguir obter o tamanho do tubo, né?
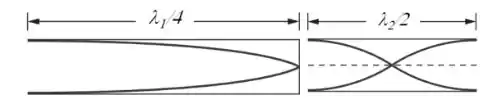
Bem, você concorda comigo que pelo desenho acima, o tamanho do tubo seria a soma dos comprimentos dados no enunciado, ou seja:
Tá, então notaram que o problema aqui é encontrarmos os comprimentos de onda necessários para cada caso?
Bem, e qual é a fórmula que correlaciona comprimento de onda com as variáveis dadas no enunciado que foram frequência e velocidade do som no ar?
O enunciado deu pra gente que e são 256 Hz e 440 Hz, respectivamente e a velocidade do som 343 m/s, então só vem comigo!!!
Passo 2
Podemos calcular qual é o comprimento de onda em cada tubo, se liga!
Analogamente para o comprimento de onda 2!
Passo 3
Pronto, agora é substituir e encontrar o tamanho do tubo hehe
TCHARAAAMMM! Mais uma questão que parece ser assustadora mas vimos juntinhos que conseguimos fazer 😊