Exercícios Resolvidos de Tubos Sonoros

Ver Teoria

Exercício 27 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45

Enunciado

UFF – Física III – VS – 2022.1 – Q6

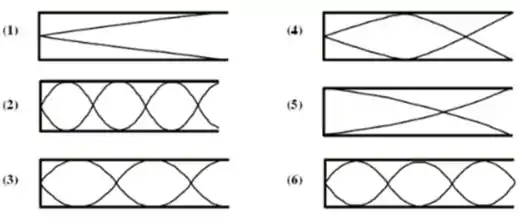
As figuras mostram ondas estacionárias em seis tubos de órgãos de mesmo comprimento. Cada tubo tem uma extremidade fechada e a outra aberta. Algumas das situações são impossíveis. Quais das figuras não mostram ondas estacionárias possíveis?

Passo 1

E aí, galerinha! Tudo na paz por aí?

Essa questão é muito legal porque ela é totalmente teórica. Primeiro de tudo é, nós temos sempre ondas que vão ser ondas ou retas...o que passar disso é procedência maligna, beleza? Hahaha

Com isso, podemos já observar que o desenho (5) representa uma onda não real já que o perfil parece mais uma curva exponencial ou logarítmica.

Outra coisa é, uma onda só poderá ter uma “contra-onda” ou seja, sua inversa perfeitamente, se o tubo for fechado dos dois lados. Percebam que esta alternativa implica dizer que a onde (6) também não é real pois ela é perfeitamente simétrica, o que só seria possível se o lado direito estivesse fechado também.

Resposta

(5) e (6)

Exercícios de Livros Relacionados

No tubo A , a razão entre a frequência de um harmônico e a frequência do harmônico precedente é 1,2 . No tubo B , a razão entre a frequência de um harmônico e a frequência do harmônico precedente é 1,

Duas ondas sonoras com uma amplitude de 12 n m e um comprimento de onda de 35 c m se propagam no mesmo sentido em um longo tubo, com uma diferença de fase de π / 3 r a d . Qual é ( a ) a amplitude e b

Na figura abaixo, F é um alto-falante alimentado por um oscilador de áudio com uma frequência que varia entre 1000 H z a 2000 H z e D é um tubo cilíndrico com 45,7 c m de comprimento e as duas extremi

Os menores tubos usados em órgãos têm 7,5c m de comprimento. (a) Estime a frequência fundamental para um tudo aberto nas duas extremidades que tenha este comprimento. (b) Para este tubo, estime o núme

Que comprimento deve ter um tubo de órgão aberto num extremo e fechado no outro para produzir, como tom fundamental, a nota dó da escala média, ν = 262H z , a 15 ° C , quando a velocidade do som no ar