Um tubo , que possui de comprimento e é aberto em suas duas extremidades, vibra na sua terceira frequência harmônica mais baixa. Outro tubo , de comprimento , é fechado em uma de suas extremidades e vibra em sua segunda frequência harmônica mais baixa. As frequências dos tubos e coincidem. Dado:
- Encontre as posições do tubo em que estão os nós de deslocamento.
- Encontre o comprimento do tubo .
Passo 1
a)
Bem, aqui a gente vai precisar usar a fórmula que relaciona o do tubo com o comprimento da onda. Para um tubo aberto, essa fórmula é:
Sendo
Ótimo! Agora podemos terminar a solução simplesmente desenhando a forma da onda estacionária em um tubo aberto. Essa é a forma mais simples de se visualizar! Vamos lá:
Uma onda estacionária num tubo aberto tem a seguinte forma:
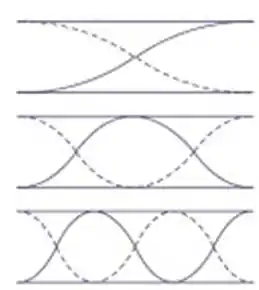
Na figura temos, em sequência, Então a forma de onda que queremos é a última, .
É fácil desenhar a forma de onda de um tubo aberto: basta a gente fazer primeiro uma “ondinha” de extensão , depois um meio comprimento completo, depois outro, e outro... quantos forem suficientes, e depois finalizar o desenho com outra “ondinha” de extensão
Beleza! A gente consegue ver claramente onde ficam os nós. Eles ficam em:
E essas são as posições dos três nós!
Passo 2
b)
Aqui a gente mata a questão simplesmente igualando as frequências, já que elas são iguais.
Mas vamos antes montar a expressão pra frequência do tubo , que é um tubo fechado:
OBSERVAÇÃO: Você também poderia encontrar a fórmula
Repare que as duas fórmulas, apesar de parecerem diferentes, são iguais. Porque em um dos casos começa em zero, e no outro em . Assim, os valores acabam sendo idênticos. Sacou?
Fim da observação.
Lembrando que queremos achar o tal do Vamos usar:
Como começa em o nosso segundo harmônico é em , logo:
E agora vamos montar a expressão pra frequência de
Logo, comparando os dois:
Resposta
a)
b)