Duas frequências de ressonância sucessivas de um tubo são 1250Hz e 1750Hz. Desprezando efeitos de borda, determine:
a) O tubo está aberto nas duas extremidades ou em apenas uma? Justifique. (A resposta sem justificativa não será considerada)
b) O comprimento do tubo
c) Para o harmônico de , esboce as curvas da pressão em função da posição ao longo do tubo. Considere o tubo aberto em e indique claramente a posição dos nós.
d) Determine a frequência do modo fundamental.
e) Para o modo fundamental, esboce as curvas do deslocamento como função de Considere o tubo aberto em e indique claramente a posição dos nós.
f) Ainda para o modo fundamental, escreva a função de onda para o deslocamento considerando que a amplitude do deslocamento é . Considere o tubo aberto em .
Passo 1
a) a frequência de ressonância sucessivas de num tubo pode ser descrita como
com
Podemos descrever a equação para os tubos como
e
Logo
São impares consecutivos! O tubo está aberto em uma extremidade.
Passo 2
b) Vimos no item anterior que , numa frequência de para a velocidade do som no ar. Logo
Passo 3
c) Temos que , sendo o comprimento total da onda
Os nós da onda se dão em
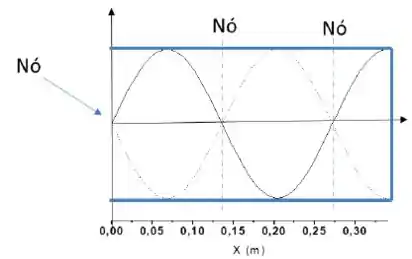
Passo 4
d)
Passo 5
e) Nó em
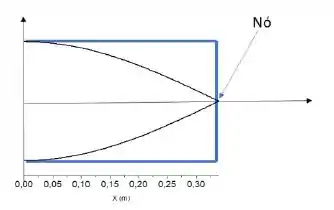
Passo 6
f)
Aplicando a relação trigonométrica
Sendo
Chegamos a equação final da função da onda
Resposta
a) O tubo está aberto em uma extremidade
b)
c)
d)
e)
f)