A figura abaixo mostra a leitura de um monitor de pressão montado em um ponto da trajetória de uma onda sonora de uma só frequência, propagando-se com uma velocidade de no ar, de massa específica homogênea . A escala do eixo vertical do gráfico representado na figura abaixo é definida por . Se, nas vizinhanças do monitor de pressão, a função deslocamento da onda é dada por .
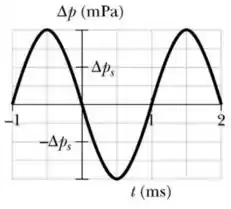
a) Determine a amplitude de pressão, , o período e o número de onda.
b) Obtenha e escreva a função que descreve o deslocamento .
c) Coloca-se um tubo com apenas uma extremidade aberta no caminho da onda sonora. Calcule qual deve ser o menor comprimento do tubo para que a onda estacionária formada em seu interior entre em ressonância.
d) Faça o desenho da onda estacionária de pressão no tubo, na situação do item c, indicando as extremidades aberta e a fechada.
e) Suponha, agora, que o monitor de pressão se encontre a uma distância da fonte sonora isotrópica (emite igualmente em todas as direções). Observa-se que a amplitude da onda de pressão é duplicada ao aproximarmos o monitor de em direção à fonte. De quanto aumenta a intensidade da onda sonora? Calcule a distância .
Passo 1
Sabemos que é a amplitude da nossa onda. Pela figura, vemos que
Como pelo enunciado
Passo 2
Pela figura vemos que o primeiro máximo (a esquerda) acontece em e que o segundo máximo (a direita) acontece em . Como o período é a diferença de tempo entre dois máximos, temos
Passo 3
Temos que o número de onda é dado por
E para achar o comprimento de onda podemos usar a relação
Como temos o período e a velocidade do som é dada pelo enunciado .
Agora podemos calcular o número de onda
Passo 4
Temos que a função deslocamento da nossa onda é dada por
.
O número de onda já calculamos no passo anterior .
Já a frequência angular podemos achar usando o período
Passo 5
Agora falta achar a amplitude .
Para uma onda sonora, a variação de pressão se relaciona com a função deslocamento por
Onde é o modo de compressibilidade do ar (já já vamos lidar com ele).
Como .
Quando , temos que , assim
Para calcular , já temos o número de onda e a variação máxima de pressão . Agora só falta
O módulo de compressibilidade se relaciona com a densidade do ar e com a velocidade de propagação da onda nesse meio por
Como, pelo enunciado, e
Então finalmente podemos calcular a nossa amplitude !
E a nossa função deslocamento será
Tudo em unidades do SI.
Passo 6
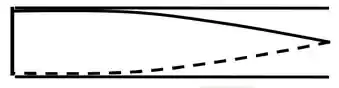
Temos que em um tubo com apenas uma extremidade aberta, haverá um nó na extremidade fechada e um anti-nó na extremidade aberta, de forma que no primeiro harmônico caberá somente um quarto de comprimento de onda dento do tubo
Passo 7
O nosso desenho fica mais ou menos assim mostrando o nó na extremidade aberta e o anti-nó na extremidade fechada
Passo 8
Vamos calcular analiticamente a intensidade sonora quando estamos perto e longe e compará-las.
A intensidade sonora é dada pela razão entre a potência média da onda sonora dividida pela área que ela atua
Quando estamos a uma distância da fonte, medimos uma intensidade e a área em que a onda passa é a área de uma esfera de raio
Agora quando estamos a uma distância da fonte (quando nos aproximamos), medimos uma intensidade que será dada por
Podemos eliminar a potência média fazendo a razão entre as duas intensidades
Passo 9
Beleza, já temos uma expressão interessante que tem a distância . Agora só falta calcular essa razão entre as intensidades.
Para isso basta lembrar que a intensidade de uma onda sonora se relaciona com a sua amplitude por
E nessa relação quando nos aproximamos somente a amplitude da onda se modificará! Ou seja, a razão entre as duas intensidades será a razão entre os quadrados das amplitudes das ondas
Como
Finalmente pelo enunciado sabemos que quando nos aproximamos a amplitude da pressão duplica, ou seja
Assim
Daqui vemos que a intensidade aumentou 4 vezes.
Então finalmente (ufa!) podemos calcular
Resposta
- , ,
- ,
-
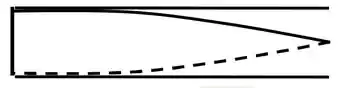
- Intensidade quadriplicou.