Exercícios Resolvidos de Tubos Sonoros

Ver Teoria

Exercício 36 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 37 38 39 40 41 42 43 44 45

Enunciado

Física 3 - UFF; P2 de 2019.2

3 - Os comprimentos de onda correspondentes aos harmônicos de um tubo de órgão que está aberto em uma extremidade e fechado na outra podem ser encontrados dizendo que o comprimento do tubo deve ser igual a

um número ímpar de múltiplos de um quarto de comprimentos de onda

um número ímpar de múltiplos de um terço de comprimentos de onda

um número ímpar de meios comprimentos de onda

um número inteiro de meios comprimentos de onda

um número inteiro de comprimentos de onda

Passo 1

Um tubo harmônico aberto em uma extremidade e fechado na outra, possui esse formato aqui:

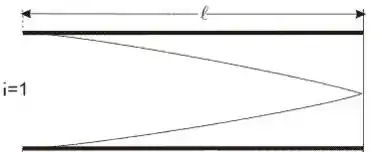
Onde esse ai representa o harmônico (nesse caso o primeiro).

De acordo com a teoria, os harmônicos permitidos aqui só são de ordem ímpar. Logo, o próximo harmônico depois desse será o terceiro e assim por diante.

Bem, o comprimento de onda em tubos aberto-fechados são dados por...

Onde é o número de harmônicos ( sempre ímpar)!

Logo, o comprimento do tubo deverá ser...

Então a letra correta é a letra A, ou seja, o comprimento do tubo () deve ser igual a um número ímpar () de múltiplos de um quarto de comprimentos de onda .

Resposta

Letra A.

Exercícios de Livros Relacionados

No tubo A , a razão entre a frequência de um harmônico e a frequência do harmônico precedente é 1,2 . No tubo B , a razão entre a frequência de um harmônico e a frequência do harmônico precedente é 1,

Duas ondas sonoras com uma amplitude de 12 n m e um comprimento de onda de 35 c m se propagam no mesmo sentido em um longo tubo, com uma diferença de fase de π / 3 r a d . Qual é ( a ) a amplitude e b

Na figura abaixo, F é um alto-falante alimentado por um oscilador de áudio com uma frequência que varia entre 1000 H z a 2000 H z e D é um tubo cilíndrico com 45,7 c m de comprimento e as duas extremi

Os menores tubos usados em órgãos têm 7,5c m de comprimento. (a) Estime a frequência fundamental para um tudo aberto nas duas extremidades que tenha este comprimento. (b) Para este tubo, estime o núme

Que comprimento deve ter um tubo de órgão aberto num extremo e fechado no outro para produzir, como tom fundamental, a nota dó da escala média, ν = 262H z , a 15 ° C , quando a velocidade do som no ar