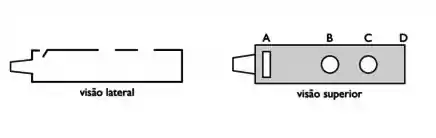
A figura mostra uma “‘flauta” simplificada, com a extremidade aberta. Há também uma grande abertura em (próxima ao bocal) e dois orifícios em e , tais que e . Sabe-se que e que a velocidade do som é Qual a frequência que se espera ouvir ao soprar a flauta com o dedo tapando ?
- Não há como excitar uma onda no tubo, já que e estão à mesma pressão externa.
- .
- .
- .
Passo 1
Bom galera, eu sei que é tentador tentar aplicar essa equação aqui nessa questão:
Mas não é por ai. Nós vamos resolver esse problema apenas lembrando das ondas de pressão que causam o som, além da geometria da flauta.
Passo 2
Bom, os pontos e estão em contato direto com a atmosfera, ou seja, representam nós de pressão. Mas a gente sabe que a onda que se forma dentro de um tubo sonoro é uma onda estacionária e que, no estado fundamental, a distância entre dois nós é dada por .
Ou seja, .
E quanto vale
O enunciado nos diz que e que . Se , então e
Logo:
Passo 3
Agora fica fácil. Já temos o comprimento de onda e a velocidade do som. Vamos achar a frequência usando:
Resposta
d)