
Um disco de borracha de se movimenta inicialmente com vetor velocidade sobre uma superfície horizontal sem atrito e sofre uma colisão com um disco de borracha de movendo-se inicialmente com vetor velocidade . Considere as seguintes situações:
a) Se o vetor velocidade e o vetor velocidade do centro de massa , calcule o vetor velocidade .
b) Suponha que o vetor velocidade e que o vetor velocidade . Suponha também que após a colisão, o disco de tem velocidade escalar igual a e faz um ângulo em relação ao eixo positivo. Determine a velocidade do disco de após a colisão.
c) Suponha finalmente que o vetor velocidade e que o vetor velocidade e que a colisão é perfeitamente inelástica. Calcule a percentagem de energia perdida nesta colisão.
Passo 1
a)
Vou fazer uma figura pra gente visualizar melhor essa letra a):
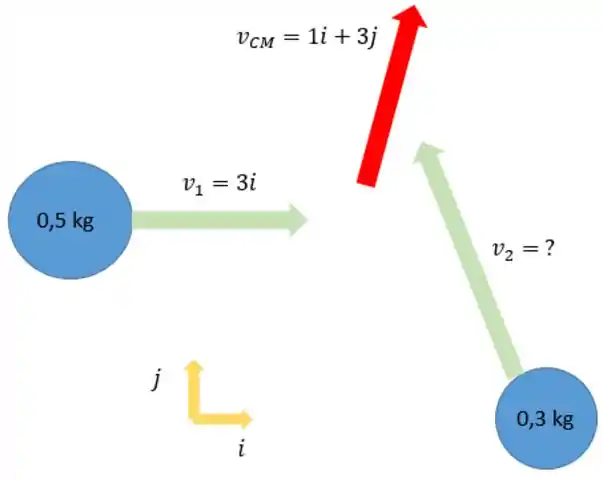
Show, vamos continuar! :D
Passo 2
Vamos aplicar a fórmula da velocidade do centro de massa!
sendo e a massa dos discos de borracha, um de e outro de . Digamos que e .
E como , vamos ter
Passo 3
Passando isso pra frações que é melhor, dá:
Passo 4
Separando da forma , isso dá:
Passo 5
E pelo enunciado, , ou seja:
Portanto, vamos ter
A primeira equação fica:
E pela segunda equação:
Portanto, .
Passo 6
b)
Agora a massa começa parada e sofre o choque da massa . Queremos achar a velocidade final da após a colisão. Dá uma olhada na figura:
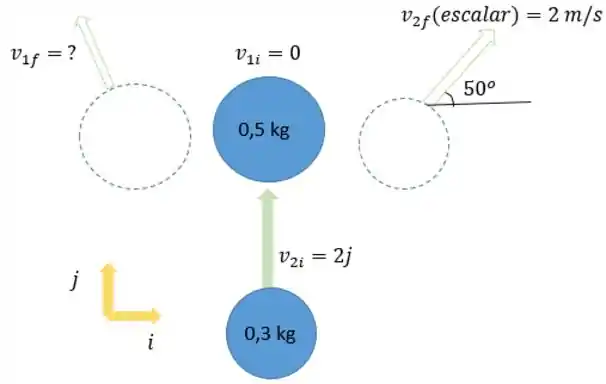
Passo 7
Pela conservação do momento linear total, temos:
E como :
Passo 8
Beleza, agora precisamos achar ! Sabemos que esse vetor faz um ângulo de com o o eixo positivo e que seu módulo é . Ou seja, afinal isso é um problema básico de trigonometria:
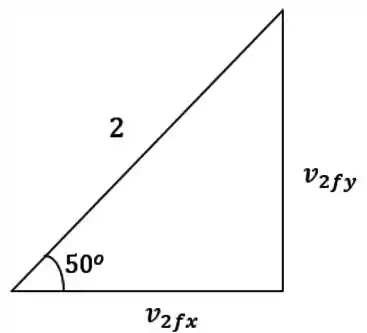
Assim,
Passo 9
Lembrando que achamos
Ou seja,
Esse seria o valor exato, mas o enunciado fornece os valores e então
Passo 10
c)
Chegamos no último caso! A colisão é totalmente inelástica, então os discos saem colados, com a mesma velocidade final . Seria mais ou menos assim:
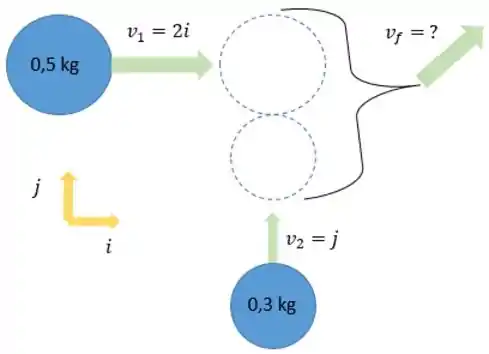
Passo 11
A equação da conservação do momento linear total fica assim:
Passo 12
Beleza, mas queremos a porcentagem de energia perdida na colisão. Por energia se entende energia cinética . E essa porcentagem é dada por
(Vou chamar de e de , beleza?)
Essa fórmula faz sentido porque se , o que ocorreria se os discos parassem, a porcentagem seria , ou seja, da energia seria perdida. Por outro lado, se tivéssemos , daria e de fato, nenhuma energia seria perdida.
Enfim, vamos calcular e !
Passo 13
As velocidades vetoriais são e mas pra calcular a energia cinética precisamos das velocidades escalares, os módulos e .
Então vamos ter
Passo 14
Agora vamos achar ! A velocidade vetorial é então a velocidade escalar é:
Assim,
Passo 15
Beleza, então agora podemos calcular a porcentagem!
Resposta
a)
b)
c)