Em uma colisão bidimensional com força resultante externa nula, duas partículas de mesma massa, , colidem elasticamente como mostra a figura. Antes da colisão a velocidade da partícula 1 é e a partícula 2 está em repouso. O ângulo da velocidade com o eixo é .
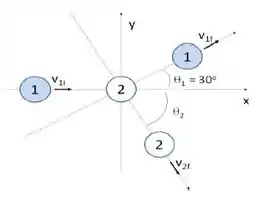
(a) Determine a velocidade da partícula 1 após a colisão.
(b) Obtenha o impulso sobre a partícula 1 durante a colisão.
(c) Encontre a velocidade inicial da partícula 2 em relação ao centro de massa do sistema.
Passo 1
Temos uma colisão bidimensional. Uma informação muito importante é que a força resultante externa no sistema é nula, pois isso significa que podemos considerar a colisão em um sistema isolado. Logo temos que o momento linear se conserva:
Além disso, ele diz que as partículas colidiram elasticamente, logo a energia cinética do sistema se conserva:
Beleza, temos um bom ponto de partida para achar qualquer informação sobre essa colisão.
Passo 2
Na letra (a), queremos a velocidade da partícula 1 após a colisão .
Como temos as massas e a velocidade inicial no sistema, podemos tentar usar a conservação do momento linear. Lembrando que podemos separar os eixos e dizer que o momento linear se conserva tanto em quanto em .
Não sabemos a velocidade final nem da partícula 1 nem da partícula 2.
Mas como temos duas equações de conservação ( e ), nós, normalmente, conseguiríamos achar essas duas incógnitas. Entretanto, não sabemos o ângulo , ou seja, mais uma incógnita. Portanto, além disso, também precisaremos usar a conservação da energia cinética.
Passo 3
Vamos começar com essas duas equações de momento linear, mas primeiro vamos decompor as velocidades nas suas componentes verticais e horizontais.
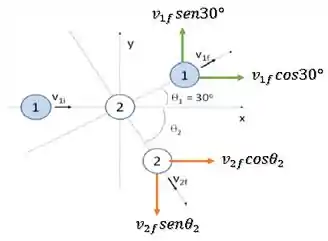
Conservando o momento linear em temos:
Já em , temos:
Passo 4
Vamos relacionar as energias cinéticas, agora. Lembrando que energia cinética é um escalar (não apresenta direção e sentido), logo devemos usar o módulo das velocidades:
Passo 5
Temos agora um sistema assim:
Esse sistema é meio chatinho de se resolver...
Não se assusta com o que eu vou fazer, segura na minha mão e vem comigo!
Quando temos uma partícula colidindo com outra em repouso, as duas sempre saem da colisão fazendo um ângulo de .

Po se eu só escutasse isso aí solto, eu também não ia aceitar de boas.
Mas olha para como ficou a equação da conservação da energia cinética:
Olha a viagem, agora...
Podemos dizer que essa relação segue o teorema de pitágoras. Lembra aquela lei que a gente quase não usa...
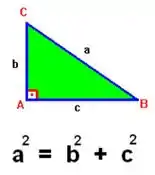
Então podemos pensar que as velocidades (b) e (c) como os catetos de um triângulo retângulo, onde a hipotenusa (a) é .
Com isso, concluimos que os vetores e fazem entre si:
Ahhhhh, que isso!
Então, a gente consegue mole:
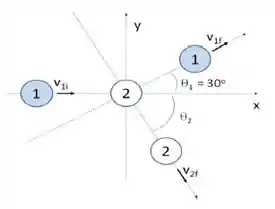
Passo 6
Agora nosso sistema melhorou um pouquinho, podemos usar:
Com a primeira equação, temos:
Substituindo esse valor na segunda equação, temos:
Passo 7
Achamos o módulo da velocidade, vamos achar, agora, as componentes em e da velocidade para responder quem é o vetor .
A componente em (horizontal) é:
Já a componente em (vertical) é:
Logo, a velocidade da partícula 1 após a colisão é:
Passo 8
Na letra (b), queremos o impulso sobre a partícula 1.
Agora que descobrimos a velocidade final de 1, repara que temos tudo que é necessário para achar a variação de momento linear dessa partícula.
Repara que no sistema não há variação de momento linear, porém, em cada partícula separadamente, temos uma variação sim.
Mas para que isso?
Lembra daquele teorema ipulso-momento linear?
Podemos aplicá-lo sobre a partícula 1:
Passo 9
Então, vamos calcular esse impulso :
Passo 10
Na letra (c), queremos a velocidade inicial da partícula 2 em relação ao centro de massa do sistema.
Como já sabemos que, inicialmente, a partícula 2 está em repouso, basta acharmos a velocidade do centro de massa e depois calcular essa velocidade relativa.
Para achar a velocidade do centro de massa, devemos fazer uma média ponderada das velocidades de cada partícula do sistema.
Vamos achar :
Substituindo os valores das velocidades, temos:
Passo 11
Bom, já temos as velocidades do centro de massa e da partícula 2 . Para achar a velocidade da partícula 2 com relação ao centro de massa, basta subtrairmos a velocidade da partícula 2 da velocidade do novo referencial (centro de massa):
Prontinho, achamos a resposta da letra (c).

Resposta
(a)
(b)
(c)