Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Velocidade e Momento Linear do Centro de Massa

Ver Teoria
Exercício 45123456789101112131415161718192021222324252627282930313233343536373839404142434446

Enunciado

UFABC – Fenômenos Mecânicos – Lista 5 – Questão 14

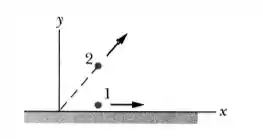
Na figura abaixo, duas partículas são lançadas da origem do sistema de coordenadas no instante t = 0 . A partícula 1 , de massa m 1 = 5,00   g , é lançada horizontalmente para a direita, em um piso sem atrito, com uma velocidade escalar de 10,0   m / s . A partícula 2 , de massa m 2 = 3,00   g , é lançada com uma velocidade escalar de 20,0   m / s e um ângulo tal que se mantém verticalmente acima da partícula 1 .

  1. Qual é a altura máxima H m á x alcançada pelo CM do sistema de duas partículas?

    2. Em termos dos vetores unitários, quais são

  2. a velocidade e
  3. a aceleração do CM ao atingir a altura máxima H m á x ?

Passo 1

Oi pessoa, tudo bem? Essa questão parece complicada, mas vou fazer passo a passo com você!

Essa é uma questão de sistema de partículas, com conceito de centro de massa. O problema pede primeiro para calcularmos a altura máxima alcançado pelo centro de massa, então precisamos determinar qual é a altura máxima das duas partículas e calcular o centro de massa.

Depois o problema pede para calcular a velocidade e aceleração do CM, e para isso vamos analisar a velocidade e aceleração e cada partícula e calcular no centro de massa.

Mas calma, vamos fazer juntos!

Passo 2

Letra (a):

Primeiro, vamos determinar a componente y da velocidade da partícula 2 ( v y ). Para tanto, devemos perceber que ele diz que a velocidade horizontal de 2 é igual a velocidade horizontal de 1 . Assim:

v 0 x 2 = v x 1 = 10   m / s

Portanto, aplicando o teorema da Pitágoras, sabemos que:

v 0 y = v 0 2 - v 0 x 2

Substituindo os valores:

v 0 y = 20 2 - 10 2 = 17,3   m / s

Beleza?

Passo 3

Como somente o peso atua sobre a partícula 2 , então podemos aplicar lei de conservação de energia para determinar a posição de y m á x alcançada pela partícula 2 , assim:

m v 0 2 2 = m g y m á x + m v 0 x 2 2

No ponto máximo, somente a componente y da velocidade é nula, porém a velocidade x é constante e, por isso, deve ser considerada quando aplicamos a lei de conservação da energia. Assim, isolando y m á x :

m g y m á x = m v 0 2 2 - m v 0 x 2 2

y m á x = 1 2 g v 0 2 - v 0 x 2

Substituindo os valores:

y m á x = 1 2 × 9,8 20 2 - 10 2 = 15,3   m

Tranquilo?

Passo 4

Para determinar o H m á x do centro de massa usaremos a seguinte relação:

H m á x = m 1 y 1 + m 2 y 2 m 1 + m 2

Como foi considerado que y = 0 corresponde a reta com a partícula 1 está se movimentando, então:

H m á x = m 2 y m á x m 1 + m 2

Substituindo os valores:

H m á x = 3 × 15,3 3 + 5 = 5,74   m

Passo 5

Letra (b): velocidade do centro de massa do CM

Como as partículas têm a mesma velocidade horizontal e a velocidade vertical da partícula 2 é nula no ponto mais alto da trajetória, então a velocidade do centro de massa se resume apenas a velocidade da partícula 1:

v → C M = 10 i ^   m / s

Passo 6

Letra (c): agora o problema pede a aceleração do centro de massa

Para determinar a aceleração do centro de massa, vamos usar a seguinte relação:

a → C M = m 1 a → 1 + m 2 a → 2 m 1 + m 2

Como a 1 = 0 e a → 2 = - 9,8 j ^   m / s 2 , então:

a → C M = 3 × ( - 9,8 j ^ ) 3 + 5 = - 3,68 j ^   m / s 2

Ufa terminamos!

E é isso! Espero ter ajudado!

Resposta

  1. H m á x = 5,74   m ;
  2. v → C M = 10 i ^   m / s ;
  3. a → C M = - 3,68 j ^   m / s 2 .

Exercícios de Livros Relacionados

Em um jogo de sinuca, a bola branca se choca com outra bola inicialmente em repouso. Após o choque, a bola branca se move com uma velocidade escalar de 3,50m / s ao longo de uma reta que faz um ângulo
Dois patinadores, um de 65k g e outro de 40k g , estão em uma pista de gelo e seguram as extremidades de uma base de 10m de comprimento e massa desprezível. Os patinadores se puxam ao longo da haste a
A Fig. 9-44 mostra um arranjo com um trilho de ar no qual um carrinho está preso por uma corda a um bloco pendurado. O carrinho tem massa m 1 = 0,600k g e o centro do carrinho está inicialmente nas co
Na Fig. 9-45 a , um cachorro de 4,5k g está em um barco de 18k g a uma distância D = 6,1m da margem. O animal caminha 2,4m ao longo do barco, na direção da margem, e para. Supondo que não há atrito en
Na Fig. 9-43, duas partículas são lançadas da origm do sistema de coordenadas no instante t = 0 . A partícula 1 , de massa m 1 = 5,00g , é lançada horizontalmente para a direita, em um piso sem atrito