Em uma dada colisão bidimensional, uma bola de bilhar de massa , deslocando-se com velocidade atinge uma segunda bola idêntica, que está inicialmente em repouso, como ilustrado na figura abaixo. Após a colisão, a primeira bola passa a deslocar-se com velocidade de módulo , em uma direção que faz um ângulo de com eixo .
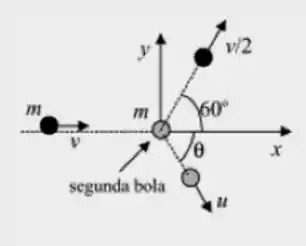
(a) Calcule o valor da velocidade da segunda bola imediatamente após a colisão (expresse seu resultado em termos de ).
(b) Tal colisão é elástica ou inelástica? Justifique quantitativamente sua resposta.
(c) Determine velocidade do centro de massa do sistema antes a depois da colisão. Justifique sua resposta.
Passo 1
a) Durante a colisão o momento linear do sistema composto pelas duas partículas é conservado. Logo, os momentos lineares do sistema imediatamente antes da colisão:
E depois da colisão:
Eles são iguais, portanto:
Igualando cada direção:
Dividindo um pelo outro, temos:
Por outro lado, se elevarmos as duas equações ao quadrado e somarmos, temos:
Logo:
Passo 2
b) A energia cinética do sistema imediatamente antes da colisão é:
Enquanto imediatamente após a colisão é:
Logo:
Com isso, podemos concluir que a colisão é elástica.
Passo 3
c) Como a resultante das forças externas é nula, não á aceleração no centro de massa e, portanto, a velocidade dele se mantém constante. Logo:
Resposta
a)
b) É elástica. A energia cinética é igual antes e depois da colisão
c)