Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Velocidade e Momento Linear do Centro de Massa

Ver Teoria
Exercício 31245678910111213141516171819202122232425262728293031323334353637383940414243444546

Enunciado

Um disco de massa m 1 = 3,0   k g , inicialmente em repouso sobre uma superfície horizontal sem atrito, sofre uma colisão não-frontal com um segundo disco de massa m 2 = 2,0   k g , movendo-se inicialmente ao longo do eixo x com velocidade escalar constante V 2 i = 2,0   m / s . Após a colisão, o segundo disco passa a ter velocidade escalar V 2 f = 1,0   m / s e sai a um ângulo θ 2 = - 60 ° em relação ao eixo x positivo, veja a figura. Use o sistema de coordenadas fornecido.

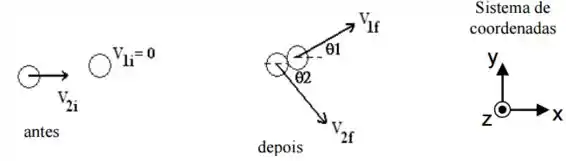
a Ache o vetor velocidade do centro de massa dos discos antes da colisão.

b Em termos dos vetores unitários i ^ e j ^ , determine o vetor velocidade V → 1 f do disco 1 após a colisão. Calcule o ângulo θ 1 com que ele emerge.

d Determine o vetor velocidade do centro de massa do sistema após a colisão, explicitamente usando seu resultado da letra b . Compare com o resultado da letra a e discuta.

Passo 1

a   Basta utilizar a fórmula para encontrar a velocidade do centro de massa:

V → C M = m 1 V → 1 i + m 2 V → 2 i m 1 + m 2

V → C M = 3,0   .   0 + 2,0   .   2,0 i ^ 3,0 + 2,0

V → C M = 0,80   i ^   m / s

Passo 2

b   Como o sistema é isolado (não há forças externas atuando e as forças internas são produzidas em par ação-reação, se anulando), a resultante das forças que age sobre o sistema é nulo e desta forma o momento linear total do sistema é conservado.

P → a n t e s = P → d e p o s i

m 1 . v → 1 i + m 2 . v → 2 i = m 1 . v → 1 f + m 2 . v → 2 f

0 + 2,0 . 2,0 i ^ = 3,0 . v → 1 f + 2,0 . v 2 f . cos ⁡ - 60 ° i ^ + v 2 f . sen ⁡ - 60 ° j ^

3,0 . v → 1 f = 4,0 - 2,0 . 1,0 . 1 2 i ^ + - 2,0 . 1,0 . - 3 2 j ^

v → 1 f = 1,0 i ^ + 3 3 j ^   m / s

Para encontrar a direção, basta imaginar um triângulo em que o eixo j ^ é o cateto oposto e o eixo i ^ é o cateto adjacente. Temos então um ângulo θ 1 com o eixo i ^ , onde:

tan ⁡ θ 1 = c a t   o p o s t o c a t   a d j a c e n t e

tan ⁡ θ 1 = 3 3 1,0

tan ⁡ θ 1 = 3 3

Logo:

θ 1 = arctan ⁡ 3 3

θ 1 = 30 °

Passo 3

  d   Podemos utilizar novamente a fórmula:

V → C M = m 1 v → 1 f + m 2 v → 2 f m 1 + m 2

Entretanto, como falamos antes, o momento linear é conservado, ou seja:

V → C M = P → M = c o n s t a n t e

Logo, a velocidade do centro de massa é sempre a mesma. Logo o resultado é igual ao da letra a .

V → C M = 0,80   i ^   m / s

Você pode substituir os dados na fórmula que vai encontrar a resposta também.

Resposta

(a) V → C M = 0,80   i ^   m / s

(b) v → 1 f = 1,0 i ^ + 3 3 j ^   m / s ; θ 1 = 30 ° ;

(d) V → C M = 0,80   i ^   m / s

Exercícios de Livros Relacionados

Em um jogo de sinuca, a bola branca se choca com outra bola inicialmente em repouso. Após o choque, a bola branca se move com uma velocidade escalar de 3,50m / s ao longo de uma reta que faz um ângulo
Dois patinadores, um de 65k g e outro de 40k g , estão em uma pista de gelo e seguram as extremidades de uma base de 10m de comprimento e massa desprezível. Os patinadores se puxam ao longo da haste a
A Fig. 9-44 mostra um arranjo com um trilho de ar no qual um carrinho está preso por uma corda a um bloco pendurado. O carrinho tem massa m 1 = 0,600k g e o centro do carrinho está inicialmente nas co
Na Fig. 9-45 a , um cachorro de 4,5k g está em um barco de 18k g a uma distância D = 6,1m da margem. O animal caminha 2,4m ao longo do barco, na direção da margem, e para. Supondo que não há atrito en
Na Fig. 9-43, duas partículas são lançadas da origm do sistema de coordenadas no instante t = 0 . A partícula 1 , de massa m 1 = 5,00g , é lançada horizontalmente para a direita, em um piso sem atrito