Dois corpos e se movem em um plano sem atrito. Suas posições variam no tempo e são dadas pelos vetores e , onde é dado em segundos e a posição em metros. O corpo tem massa e o corpo tem massa . Num dado instante de tempo, os dois corpos se chocam em uma colisão perfeitamente inelástica. Após a colisão, o vetor velocidade do conjunto faz um ângulo com a horizontal.
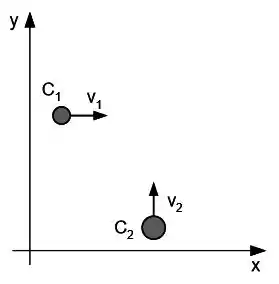
Calcule:
a) O vetor posição do centro de massa do sistema quando .
b) O vetor velocidade do centro de massa dos corpos na iminência da colisão.
c) O ângulo e o módulo da velocidade logo após a colisão.
d) A força que faz em durante a colisão que durou um décimo de segundo.
Passo 1
a)
Considerando os vetores posição das duas bolinhas temos:
Logo
Logo
O vetor é:
Passo 2
b)
Derivando cada vetor posição e obtemos os vetores e .
Usando a definição de velocidade do centro de massa obtemos:
Passo 3
c)
No sistema não há forças externas, portanto, podemos usar a conservação do momento linear para calcular o ângulo após a colisão. Esta colisão é completamente inelástica:
Momento linear no eixo :
Momento linear no eixo :
Fazendo encontramos a :
Para calcular a velocidade final após a colisão usamos ou
Passo 4
d)
O sistema é livre de forças externas, porém existem duas forças internas que podem ser calculadas, isto é:
Calculando a variação do momento linear:
Substituindo na fórmula da força:
Resposta
a)
b)
c) ;
d)