Um cachorro de massa encontra-se parado na extremidade de um barco de massa () distribuída uniformemente em seu comprimento . O sistema encontra-se em repouso em um lago de águas calmas. Em um dado momento o cachorro se movimenta para a outra extremidade. Uma menina observa a situação às margens do lago, em repouso. Desprezando o atrito entre o barco e as águas do lago é incorreto afirmar que:
(a) O centro de massa do sistema barco-cachorro permanece em repouso durante o trajeto do cachorro.
(b) Para a menina o cachorro permanece em repouso enquanto o barco se move sobre as águas do lago.
(c) Para a menina, durante o trajeto do cachorro, o barco se movimenta no sentido oposto.
(d) Para a menina, o cachorro se move mais do que o barco.
(e) O momento linear do sistema cachorro-barco se conserva.
Passo 1
Se o atrito com a água é desprezível, o sistema (barco+cachorro) está livre da ação de forças externas.
Logo, como o sistema é isolado, o momento linear se conserva:
Mas como o sistema está em REPOUSO inicialmente, a posição do centro de massa vai se manter SEMPRE no mesmo lugar.
Mas como isso acontece?
Bom, se tivéssemos apenas o barco uniforme, o centro de massa do sistema estaria em seu centro...
Mas como também temos o cachorro, o centro de massa está levemente deslocado do centro:
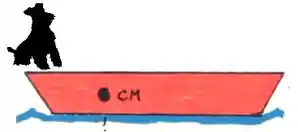
Já vimos que como não tem nenhuma força externa resultante agindo sobre o sistema, esse centro de massa deve continuar na mesma posição.
Então, quando o cachorro se desloca para a direita o que acontece é um par de ação e reação (forças internas).
O cachorro empurra o barco para a direita enquanto o barco empurra o cachorro para a esquerda...

De forma que cada um se desloca no sentido contrário do outro, mantendo o centro de massa no mesmo lugar:
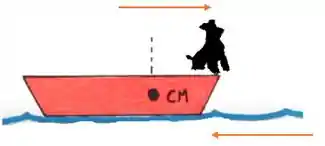
Vamos encontrar a afirmativa incorreta.
Passo 2
(a) O centro de massa do sistema barco-cachorro permanece em repouso durante o trajeto do cachorro.
Como não há nenhuma força externa resultante atuando sobre o sistema, seu momento linear é constante.
Ou seja, se ele está em repouso inicialmente, ele continua em repouso.
A ideia é que os momentos lineares do cachorro e do barco se anulam de forma a manter o momento linear do sistema nulo.
Passo 3
(b) Para a menina o cachorro permanece em repouso enquanto o barco se move sobre as águas do lago.
Vimos que observando o sistema de fora, tanto o cachorro quanto o barco se movimentam (em direções opostas).
Ficamos com a letra (b), incorreta.
Mas vamos passar rapidinho pelas outras afirmativas...
Passo 4
(c) Para a menina, durante o trajeto do cachorro, o barco se movimenta no sentido oposto.
(e) O momento linear do sistema cachorro-barco se conserva.
Estão corretíssimas!
Os dois se movimentam em sentidos opostos de forma a manter o momento linear total do sistema constante.
Passo 5
(d) Para a menina, o cachorro se move mais do que o barco.
Bom nesse caso, a velocidade de cada um vai depender de sua massa.
Como o momento linear do sistema é nulo (repouso), os momentos lineares dos dois se anulam:
Como a massa do barco é maior que a do cachorro , a sua velocidade é menor que a do cachorro .
Resposta
Letra (b)