UERJ, Sem Campus, Cálculo II, Provas de Cálculo 2 - Profº Filipe Iorio - P1 2023.1, Questão 1a
1) Considere a relação definida pela equação
a. Determine e esboce o maior subconjunto na qual a relação pode ser uma função real.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema foi dada a função e nosso objetivo é obter o maior subconjunto em que seja real.
Lembra como fazemos isso? 🤔
De forma simplificada, o que temos que fazer é definir os valores de , e de modo que seja uma função real.
Pra isso, temos que analisar a função e verificar quais as restrições que temos.
Sacou? Bora começar! 😉
Passo 2
A função é dada por
Nesse caso, podemos observar a partir do termo que o conteúdo dentro da raiz tem que ser maior ou igual a , ou seja
Já pelo termo sabemos que só existe se .
Dessa forma, temos que pode ser definido como
Esboçando a região , temos
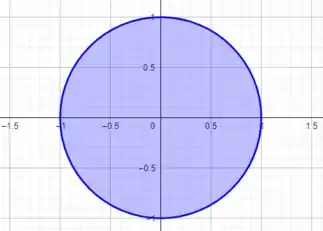
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍