UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cálculo 2 - Profº Ronie Peterson - Lista de Exercícios 1, Questão 1a
Encontre uma função de várias variáveis que represente:
- O volume de um paralelepípedo retângulo de dimensões e.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para encontrarmos uma função de várias variáveis que represente o volume de um paralelepípedo retângulo de dimensões e , ou seja:
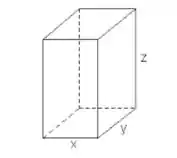
E aí? Como podemos fazer isso?
Passo 2
Bom... sabemos que o volume de um paralelepípedo é dado pela multiplicação de suas arestas.
Nesse caso, vemos que as arestas correspondentes são e .
Dessa forma, temos o volume :
Como o volume depende do valor de cada aresta, temos então a função do volume:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Fazer um esboço de algumas superfícies de nível da função w = x 2 + y 2 + z 2 . O que ocorre com os valores da função ao longo de semi-retas que partem da origem?
Identificar as afirmações verdadeiras:g) Todo ponto de acumulação de um conjunto A pertence a esse conjunto.
10- Considerando a função z = f x ,y = 7 - x 2 + y 2 ,0 ≤ x 2 + y 2 ≤ 16 , 25 - x 2 - y 2 ,16 ≤ x 2 + y 2 ≤ 25 b)Identifique a curva de nível que contém o pontoP 0 = ( 1 ,3 ) .
Encontrar uma função de várias variáveis que nos dê:e) O volume de um paralelepípedo retângulo de dimensão x , y e z .
Encontrar uma função de várias variáveis que nos dê:o comprimento de uma escada apoiada como na figura 1.35.