4. A temperatura em um ambiente com solo plano não depende da altura. Fixando no solo uma origem, o eixo apontando para leste e o eixo para norte, ela é dada por
b. Se você sair de qualquer ponto em direção ao sudoeste, qual será a variação de temperatura?
Passo 1
Oi, galerinha! Tudo bom? O problema nos forneceu uma superfície, onde a temperatura é função da sua posição no plano , dada por:
E ele quer saber como sera a nossa variação de temperatura, ou seja, nosso se caminharmos para o sudoeste.
Então para entender como será essa variação, a primeira coisa a fazer é saber que direção é essa e depois interpretar esse resultado!
Passo 2
Então, galerinha, a direção sudoeste é essa aqui,
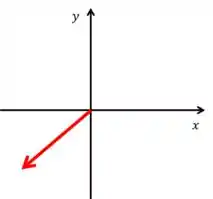
Ou seja, seguindo a direção desse vetor, temos que a nossa variação em e sempre serão negativas.
Agora vamos analisar cada caso!
Passo 3
Temos a seguinte equação da temperatura,
Logo,
Agora queremos saber, se essa variação será positiva ou negativa. Então vamos igualar a zero e comparar e
Ou seja,
Se , temos que e se temos que .
Resposta
- Para , temos que .
- Para temos que .