Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Interferência de Ondas Sonoras

Ver Teoria
Exercício 241234567891011121314151617181920212223252627282930313233343536

Enunciado

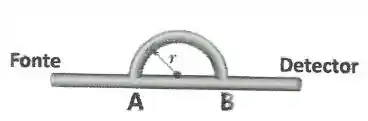
Um som de comprimento de onda λ e frequência ω se propaga para a direita a partir de uma fonte e através de um tubo que, a partir do ponto A, é formado por uma porção reta e uma semicírculode raio r. Parte da onda sonora se propaga em linha reta até o detector (ver figura). O resultado da superposição do som produz uma interferência. Dê suas respostas em termos de π.

a) Calcule a diferença de fase entre as duas frentes de onda no ponto B.

b) Calcule o menor valor de r que resulta em uma intensidade de som mínima no detector.

c) Calcule o menor valor de r que resulta em uma intensidade de som máxima no detector.

Passo 1

a) A gente tem uma fórmula pra diferença de fase! Ela é:

∆ φ = 2 π λ ∆ L

Beleza! Olhando pra essa fórmula, o comprimento de onda é conhecido. Então só precisamos calcular o ∆ L ! Ele é a diferença de comprimento entre os caminhos percorridos pelas ondas, nesse caso vai ser:

∆ L = π r - 2 r

Então:

∆ φ = 2 π λ ( π r - 2 r )

∆ φ = 2 π r λ ( π - 2 )

Passo 2

b) Pra intensidade mínima nós precisamos ter interferência destrutiva! Lembra da fórmula pra interferência destrutiva? Ela é assim:

∆ φ = ( 2 m + 1 ) π

Com m = 0 ,   1 ,   2 ,   3 …

Como ele quer o menor valor de r nós vamos usar o menor valor de m! Então:

∆ φ = 2 m + 1 π = π

π = ∆ φ = 2 π r λ ( π - 2 )

r = λ 2 ( π - 2 )

Passo 3

c) Aqui o raciocínio é parecido, só que agora teremos interferência construtiva. A fórmula é:

∆ φ = 2 m π

Mais uma vez, vamos usar o menor valor de m. Mas m não pode ser zero, porque isso daria raio zero! Então vamos usar m = 1.

∆ φ = 2 m π = 2 π

2 π = ∆ φ = 2 π r λ ( π - 2 )

r = λ ( π - 2 )

Resposta

a) ∆ φ = 2 π r λ ( π - 2 )

b) r = λ 2 ( π - 2 )

c) r = λ ( π - 2 )

Exercícios de Livros Relacionados

A figura mostra duas fontes pontuais F 1 e F 2 que emitem sons de comprimento de onda λ = 2,00m . As emissões são isotrópicas e em fase; a distância entre as fontes é d = 16,0m . Em qualquer ponto P s
Uma onda sonora senoidal se propaga no ar, no sentido positivo de um eixo x , com uma velocidade de 343 m / s . Em um certo instante, a molécula A do ar está em seu deslocamento máximo no sentido nega
Na figura abaixo temos as ondas sonoras A e B , de mesmo comprimento de onda λ , estão inicialmente em fase e se propagam para a direita, como indicam os dois raios. A onda A é refletida por quatro su
Duas ondas sonoras, produzidas por duas fontes diferentes de mesma frequência, 540H z , se propagam na mesma direção e no mesmo sentido a 330m / s . As fontes estão em fase. Qual é a diferença de fase
Na figura, um som com um comprimento de onda de 40,0c m se propaga para a direita através de um tubo que possui uma bifurcação. Ao chegar à bifurcação, a onda se divide em duas partes. Uma parte se pr