Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
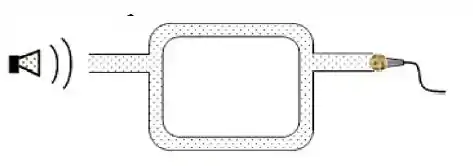
Um alto-falante gera uma onda de . Conforme mostrado na figura, o som se propaga dentro de um tubo que se divide em dois segmentos, um maior que o outro. As ondas sonoras se recombinam, antes de serem detectadas por um microfone. A velocidade do som no ar é de . Qual é a diferença mínima nos comprimentos dos dois caminhos entre os dois segmentos para que as ondas cheguem exatamente fora de fase no microfone?
Passo 1
Vamos usar a fórmula:
Já que devemos gerar uma interferência fora de fase, ou seja, destrutiva.
Para :
Passo 2
Podemos calcular
Assim:
Resposta
b)
Exercícios de Livros Relacionados
A figura mostra duas fontes pontuais F 1 e F 2 que emitem sons de comprimento de onda λ = 2,00m . As emissões são isotrópicas e em fase; a distância entre as fontes é d = 16,0m . Em qualquer ponto P s
Uma onda sonora senoidal se propaga no ar, no sentido positivo de um eixo x , com uma velocidade de 343 m / s . Em um certo instante, a molécula A do ar está em seu deslocamento máximo no sentido nega
Na figura abaixo temos as ondas sonoras A e B , de mesmo comprimento de onda λ , estão inicialmente em fase e se propagam para a direita, como indicam os dois raios. A onda A é refletida por quatro su
Duas ondas sonoras, produzidas por duas fontes diferentes de mesma frequência, 540H z , se propagam na mesma direção e no mesmo sentido a 330m / s . As fontes estão em fase. Qual é a diferença de fase
Na figura, um som com um comprimento de onda de 40,0c m se propaga para a direita através de um tubo que possui uma bifurcação. Ao chegar à bifurcação, a onda se divide em duas partes. Uma parte se pr