PUCRIO – Física 2 – 2020.1 – G2 – M. Escolha
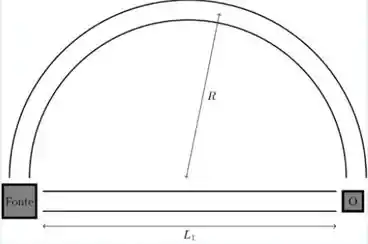
. Uma onda sonora com frequência é emitida de uma fonte posicionada como mostra a figura. A velocidade do som no meio é . O observador, também posicionado na figura, detecta uma onda sonora proveniente da interferência entre as ondas sonoras provenientes da fonte que realizam os diferentes caminhos marcados. Encontre qual a diferença de fase que o observador mede dado que e .
.
.
.
.
.
Passo 1
Vem que a gente vai detonar essa questão!
Ele quer saber a diferença de fase entre as ondas que chegam em causada pela diferença de caminho entre as ondas da fonte.
A relação entre a diferença de caminho entre as ondas e a diferença de fase que elas vão ter em um ponto qualquer é da seguinte maneira:
Então temos que saber a diferença de caminho e o comprimento de onda . Para a diferença de caminho basta fazer a diferença entre os percursos das ondas e para achar vamos usar que:
Mãos a obra então!
Passo 2
Vamos primeiro encontrar a diferença de caminho .
O percurso feito por uma das ondas é igual a e o percurso feito pela outra é igual a metade do comprimento de uma circunferência de raio , assim temos que:
Temos então que:
Passo 3
Agora vamos achar , temos:
Logo:
Passo 4
Agora só falta calcular a diferença de fase, dada por:
Assim temos que:
Com isso vemos que a alternativa correta é a letra .