PUCRIO – Física 2 2020.2 – P2 – Questão 3
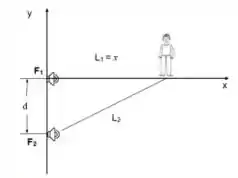
Na figura abaixo, dois alto-falatntes e estão separados por uma distância em um palco ao ar livre. Durante o teste de som, os dois alto-falantes emite, em fase, sons com comprimento de onda de . Um ouvinte encontra-se inicialmente sobre o eixo a do alto-falante e desloca-se sobre esse eixo em direção a . Considere apenas os valores . Encontre a primeira posição do ouvinte em que a intensidade sonora passa por um mínimo (interferência destrutiva)?
Escolha uma:
- Nenhuma das alternativas
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou ajudar você!
Aqui temos uma interferência destrutiva, e a equação que rege esse fenômeno é:
Como queremos a primeira posição onde isso ocorre, :
Beleza até aqui?
Passo 2
O comprimento é , e pelo desenho o comprimento pode ser encontrado pela fórmula de Pitágoras:
Daí a fórmula da interferência destrutiva fica:
Agora precisamos manipular matematicamente essa expressão para determinar o valor de . Vou começar passando para o lado direito da equação:
E agora vou elevar ao quadrado dos dois lados:
Simplificando e isolando temos:
Passo 3
Os dados são:
Agora é só substituir:
Olhando as alternativas, a correta é a (b).
Espero ter ajudado!