Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
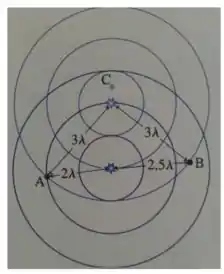
Na figura abaixo, temos 2 fontes idênticas emitindo ondas circulares no plano. No ponto C da figura, a interferência é:
- Totalmente construtiva.
- Parcialmente construtiva.
- Totalmente destrutiva.
- Parcialmente destrutiva.
- Não há interferência no ponto C.
Passo 1
Pra descobrir se a interferência é totalmente construtiva ou destrutiva, precisamos calcular . Pra isso, vamos ter que contar quantas frentes de onda tem de cada fonte até o ponto
Passo 2
Para a fonte de cima, a que está mais próxima do ponto , podemos contar uma frente de onda. Assim:
Já a partir da fonte de baixo até o ponto podemos contar frentes de onda:
Assim:
Assim:
Assim, a interferência é totalmente construtiva.
Resposta
a)
Exercícios de Livros Relacionados
A figura mostra duas fontes pontuais F 1 e F 2 que emitem sons de comprimento de onda λ = 2,00m . As emissões são isotrópicas e em fase; a distância entre as fontes é d = 16,0m . Em qualquer ponto P s
Uma onda sonora senoidal se propaga no ar, no sentido positivo de um eixo x , com uma velocidade de 343 m / s . Em um certo instante, a molécula A do ar está em seu deslocamento máximo no sentido nega
Na figura abaixo temos as ondas sonoras A e B , de mesmo comprimento de onda λ , estão inicialmente em fase e se propagam para a direita, como indicam os dois raios. A onda A é refletida por quatro su
Duas ondas sonoras, produzidas por duas fontes diferentes de mesma frequência, 540H z , se propagam na mesma direção e no mesmo sentido a 330m / s . As fontes estão em fase. Qual é a diferença de fase
Na figura, um som com um comprimento de onda de 40,0c m se propaga para a direita através de um tubo que possui uma bifurcação. Ao chegar à bifurcação, a onda se divide em duas partes. Uma parte se pr