PUCRIO – Física 2 – 2020.1 – G2 – Discursiva
Parte
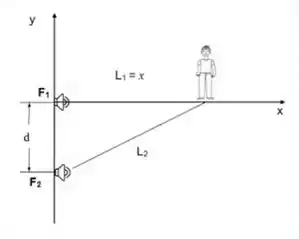
Na figura abaixo, dois alto-falantes e estão separados por uma distância em um palco ao ar livre. Durante o teste de som, os dois alto-falantes emitem, em fase, sons com comprimento de onda de . Um ouvinte encontra-se inicialmente sobre o eixo a do alto-falante e desloca-se sobre esse eixo em direção a . Considere apenas os valores . Encontre a primeira posição do ouvinte em que a intensidade sonora passa por um mínimo (interferência destrutiva)?
Passo 1
Vem comigo que vamos resolver essa juntos!
O enunciado quer a primeira posição em que do ouvinte onde teremos uma interferência destrutiva.
Para isso temos que lembrar que a interferência destrutiva entre duas ondas ocorre quando a diferença de caminho entre elas é igual a um múltiplo semi-inteiro do comprimento de onda das ondas, então temos que ter:
Onde , assim a primeira interferência destrutiva ocorre para .
Sabendo disso temos que encontrar os valores de e cuja diferença seja igual ao valor do lado direito da equação para .
Mas aí você se pergunta. Temos duas incógnitas e apenas uma equação, como vamos achar os valores de e ? Para resolver isso vamos usar o fato de que as distâncias , e formarem um triângulo retângulo, logo:
Sabendo disso poderemos encontrar a posição do ouvinte. Vamos lá então!
Passo 2
Então temos o seguinte:
Substituindo os valores de e , temos:
Agora vamos elevar os dois lados ao quadrado, assim:
Com isso temos que:
Passo 3
Agora que temos o valor de , podemos encontrar , temos:
Com isso temos que:
Prontinho, encontramos a posição do ouvinte!