I. Considere uma fonte sonora F e um detector D, posicionados conforme a figura. Admita que D receba o som de F pelos caminhos 1 (direito) e 2 (com reflexão). Considere que na reflexão há uma mudança de fase de .
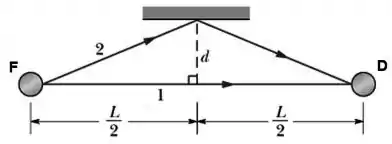
Sendo L= 8,00 m, 85 Hz a frequência das ondas e 340m/s a velocidade do som, obtenha o menor valor de d (diferente de zero) para que ocorra no detector:
a) interferência construtiva;
b) interferência destrutiva;
Passo 1
A diferença de fase entre as duas ondas vai surgir porque elas percorrem caminhos diferentes.
A diferença de fase () devido a uma diferença de caminho percorrido () é:
Onde a interferência é construtiva se , , e destrutiva para , para .
Precisamos do comprimento de onda (), que pode ser calculado pela expressão:
Passo 2
O caminho 1 possui um comprimento .
Para calcular o comprimento da caminho 2, precisamos usar Pitágoras entre e .
A diferença de caminho percorrido é, então:
A diferença de fase entre as ondas vai ser gerada pela diferença de caminho percorrido, mais a diferença de fase () gerada pela reflexão no caminho 2. Então,
Passo 3
a) O menor valor para que a interferência seja construtiva () é . Pois resultaria em .
Juntando as equações:
Elevando ao quadrado dos dois lados, pra se livrar dessa raíz:
Como e , então
Passo 4
b) O menor valor para que a interferência seja destrutiva () é . Pois resultaria em .
Elevando ao quadrado dos dois lados:
Resposta
a) 3m
b)