Exercícios Resolvidos de Interferência de Ondas Sonoras

Exercício 20 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

Enunciado

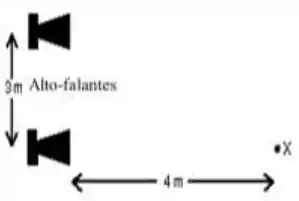
Dois pequenos alto-falantes são ligados (em fase) à mesma fonte de sinal. Os alto-falantes estão separados por uma distância de 3,0 m. Um observador se encontra no ponto X, com o ouvido na mesma altura dos alto-falantes e em frente de um deles, a uma distância de 4,0 m, como mostra a figura. Se os sons emitidos pelos alto-falantes têm a mesma amplitude, a

intensidade do som ouvido pelo observador é a menor possível quando o comprimento de onda é:

1 m

2 m

3 m

4 m

5 m

Passo 1

O som dos auto-falantes vão sofrer interferência no ponto X.

Como os dois percorrem distâncias diferentes, a diferença de caminho percorrido causará uma diferença de fase entre as ondas da seguinte forma:

Onde é a diferença de fase gerada, é a diferença de caminho percorrido entre as ondas, e o comprimento de onda.

Para que a intensidade ouvida seja a menor possível, então estamos falando de interferência destrutiva entre as ondas.

Para que a interferência seja destrutiva, uma onda tem que estar no máximo quando a outra estiver no mínimo, isso acontece quando ou qualquer múltimo ímpar de .

Onde

Passo 2

O som auto-falante mais próximo vai andar até o ponto X. Já o auto-falante mais distante vai andar:

A diferença de caminho percorrido será

Para que a interferência seja destrutiva, então:

Resposta

b) 2 m

Exercícios de Livros Relacionados

A figura mostra duas fontes pontuais F 1 e F 2 que emitem sons de comprimento de onda λ = 2,00m . As emissões são isotrópicas e em fase; a distância entre as fontes é d = 16,0m . Em qualquer ponto P s

Uma onda sonora senoidal se propaga no ar, no sentido positivo de um eixo x , com uma velocidade de 343 m / s . Em um certo instante, a molécula A do ar está em seu deslocamento máximo no sentido nega

Na figura abaixo temos as ondas sonoras A e B , de mesmo comprimento de onda λ , estão inicialmente em fase e se propagam para a direita, como indicam os dois raios. A onda A é refletida por quatro su

Duas ondas sonoras, produzidas por duas fontes diferentes de mesma frequência, 540H z , se propagam na mesma direção e no mesmo sentido a 330m / s . As fontes estão em fase. Qual é a diferença de fase

Na figura, um som com um comprimento de onda de 40,0c m se propaga para a direita através de um tubo que possui uma bifurcação. Ao chegar à bifurcação, a onda se divide em duas partes. Uma parte se pr