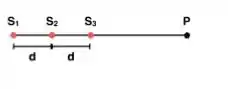
A figura ao lado mostra três fontes sonoras pontuais isotrópicas uniformemente separadas ao longo de um eixo . As fontes emitem sons de mesmo comprimento de onda λ, mesma amplitude e estão em fase. Um ponto é mostrado sobre o eixo . Suponha que quando as ondas se propagam até suas amplitudes se mantêm praticamente constantes. Qual é a amplitude de onda resultante em se a distância mostrada na figura for, respectivamente, λ/4, λ/2 e λ?

Passo 1
A amplitude resultante em P será a soma das três amplitudes:
Onde, vamos usar a relação que
Observando as equações, vemos que o e irão funcionar igual constantes de fase, eles vão determinar se as interferência será construtiva (soma) ou destrutiva (subtração).
O primeiro caso é
Assim, as “constantes de fase” serão:
Agora se lembrarmos que , observamos que a onda 1 e 3 irão se anular.
Sendo assim, a amplitude resultante e P será a amplitude de .
Passo 2
Agora para , as “constantes de fase” serão:
Agora, a onda 1 anulará a onda 2 e assim, a amplitude em P será apena a amplitude de
Passo 3
Por último quando ,
Como , então nesse caso a interferência dos três será construtiva e assim,
Resposta
Alternativa