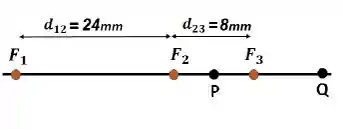
A figura ao lado mostra três fontes sonoras pontuais (F1,F2 e F3). As fontes emitem sons idênticos simultaneamente, em todas as direções, com comprimento de onda λ = 16 mm e amplitude Sm = 1 mm. Considere que a distância entre as fontes 1 e 2, e a distância entre as fontes 2 e 3 são iguais a d12 = 24 mm e d23 = 8 mm respectivamente. Dois pontos P e Q são mostrados na figura. Considere que o ponto P se encontra equidistante às fontes 2 e 3. Marque a alternativa que corresponde às amplitudes da onda resultante em P e Q respectivamente:
a)
b)
c)
d)
e)
f)
g)
h)
i)
Passo 1
No ponto P as ondas geradas pelas fontes 2 e 3 interferem construtivamente entre si, porque:
Então m = 0, interferência totalmente construtiva e a amplitude vai ser igual a 2 mm (soma das duas).
A fonte 1, porém, interfere destrutivamente no ponto P. Porque:
Então a amplitude no ponto P vai ser:
Passo 2
No ponto Q as fontes 2 e 3 interferem destrutivamente. Porque:
Repare aí que a diferença entre as distâncias percorridas pelas ondas das fontes 2 e 3 vai ser sempre 8 mm, independente da posição do ponto Q (considerando que ele esteja depois da fonte 3).
Essa interferência totalmente destrutiva no ponto Q entre as fontes 2 e 3 vai fazer com que a amplitude nesse ponto seja a amplitude da onda emitida pela fonte 1. Ou seja, a amplitude em Q vai ser:
Resposta
Letra A.