Dois alto-falantes posicionados em um plano estão separados verticalmente por e em fase um com o outro. Ambos emitem ondas sonoras de em um ambiente onde a velocidade do som é . Um ouvinte encontra-se parado à frente dos alto-falantes e a acima da reta que passa pelo ponto médio entre os mesmos. Nesse ponto onde está o ouvinte, a interferência é totalmente construtiva, totalmente destrutiva ou intermediária? Como mudará a situação se os alto-falantes estiverem fora de fase?

1. Totalmente Destrutiva; Totalmente Construtiva.
2. Totalmente Construtiva; Totalmente Destrutiva.
3. Totalmente Destrutiva; Intermediária.
4. Intermediária; Totalmente Destrutiva.
5. Totalmente Construtiva; Intermediária

Primeiro, vamos calcular

E quanto vale a diferença? Bom, pelo enunciado, o observador se encontra próximo dos alto falantes e a acima do ponto médio da distância entre as fontes. Podemos desenhar isso assim:

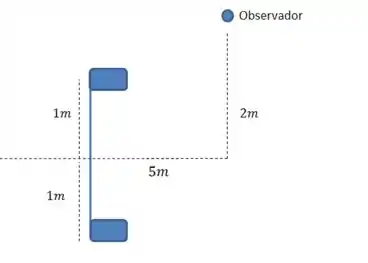
Então as distâncias do observador até cada uma das fontes são as distâncias abaixo:

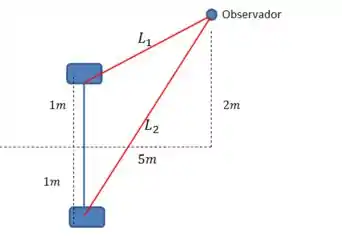
será a hipotenusa do triângulo acima. Um dos lados tem ( e o outro

E será a hipotenusa do triângulo de lado e

Assim:

Assim:

Como deu , podemos dizer que a interferência é totalmente destrutiva:

Assim, se as fontes estiverem em oposição de fase, a situação acima se inverte completamente: A interferência passa a ser totalmente construtiva.

Assim:

a)