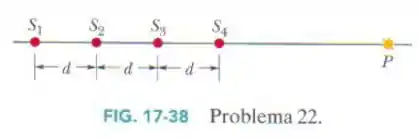
A Fig. 17-38 mostra quatro fontes sonoras pontuais isotrópicas uniformemente espaçadas ao longo de um eixo . As fontes emitem sons de mesmo comprimento de onda e mesma amplitude e estão em fase. Um ponto é mostrado sobre o eixo . Suponha que quando as ondas se propagam até a amplitude se mantém praticamente constante. Que múltiplo de corresponde à amplitude da onda resultante em se a distância mostrada na figura é (a) , (b) , (c) ?
Passo 1
O enunciado pede para desconsiderarmos a redução da amplitude com a distância, portanto, iremos analisar somente a interferência causada pelas 4 fontes em fase. Então vamos relembrar a relação da interferência com a diferença de caminho:
Passo 2
- Com , temos que:
- Já para , o mesmo fenômeno acontece, mas com os pares 1ª – 2ª e 3ª – 4ª. Logo:
- Com a história é diferente: a 1ª e a 2ª fonte irão emitir ondas que chegaram em fase em .
Como é inteiro, parece que ele não se encaixa em nenhum caso, né? Calma! Se liga na distância entre a 1ªe a 3ª fonte, ela vale , ou seja:
Portanto, elas vão agir destrutivamente, fazendo com que as ondas dessas duas fontes não cheguem em . Perceba que o fenômeno acontece da mesma maneira para a 2ª e 4ª fonte. Logo:
Passo 3
Passo 4
E mais! O mesmo fenômeno irá acontecer com a 2ª e 3ª fonte, bem como a 3ª e a 4ª. Ou seja, a amplitude que chega ao ponto é 4 vezes maior que a amplitude original.