Plano tangente e reta normal
Considere a função
- Esboce a superfície de nível que passa pelo ponto .
- Determine o ponto de interseção da reta normal a que passa pelo ponto , com o plano .
- Encontre os pontos da superfície nos quais o plano tangente a é paralelo ao plano .
Passo 1
a)
Para achar a curva de nível devemos achar primeiro onde
Então a curva de nível vai ser
Passo 2
Já vimos que uma curva desse tipo é um elipsoide. O seu gráfico fica
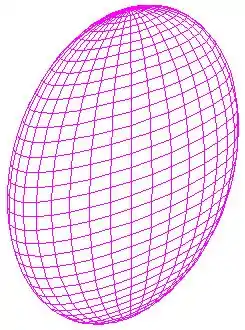
Passo 3
Para achar a reta normal devemos achar o vetor normal . Começamos achando o gradiente de
O vetor normal vai ser
Passo 4
A reta normal vai ser
Passo 5
Quando a reta passar no plano , vamos ter . Conseguimos achar o valor de para isso
Passo 6
O ponto vai ser
Passo 7
c)
O vetor normal a superfície também vai ser normal ao plano. Vamos então fazer
O vetor normal ao plano vai ser
Passo 8
Temos
Os vetores normais são proporcionais
E vamos encontrar
O ponto vai ser
Passo 9
Precisamos achar esse , vamos substituir esse ponto na equação da superfície
Então os pontos vao ser
Resposta
Exercícios de Livros Relacionados
Encontre uma equação (a) do plano tangente e (b) da reta normal à superfície dada no ponto especificado. x - z = 4a r c t g y z 1 + π ,1 ,1
Encontre uma equação (a) do plano tangente e (b) da reta normal à superfície dada no ponto especificado. 2 x - 2 2 + y - 1 2 + z - 3 2 = 10 3,3 , 5
Encontre uma equação (a) do plano tangente e (b) da reta normal à superfície dada no ponto especificado. y = x 2 - z 2 4,7 , 3
Determine as equações do plano tangente e da reta normal ao gráfico da função dada, no ponto dado. f x , y = 3 x 3 y - x ye m1 , - 1 , f 1 , - 1