Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Reta Normal

Ver Teoria
Exercício 181234567891011121314151617192021222324252627282930

Enunciado

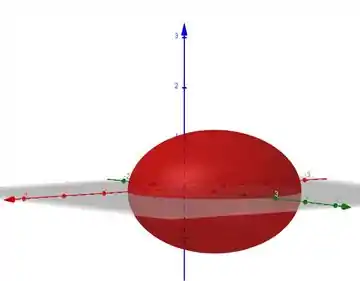
Considere

f x , y , z = x 2 + y 2 - 2 y + 2 z 2

Sabendo que x 2 + y 2 - 2 y + 2 z 2 > 0 .

  1. Esboce a superfície S de nível 2 , ou seja

    2. S = x , y , z ∈ R 3 ; f x , y , z = 2

    Identifique S como sendo um cone ou um paraboloide ou um hiperboloide ou um elipsoide ou uma esfera.

  2. Seja S a superfície do item ( a ) . Encontre a equação cartesiana do plano tangente à superfície S no ponto ( 1 , 1,1 ) , explicitando o vetor normal neste ponto.
  3. Encontre uma equação paramétrica da reta normal a superfície S no ponto ( 1,1 , 1 ) .

Passo 1

a )

Para encontrar a superfície de nível basta igualar a função a uma constante, que no nosso caso, a questão já diz que é o zero:

f x , y , z = 2

⇒ x 2 + y 2 - 2 y + 2 z 2 = 2

Tirando a raiz dos dois lados:

x 2 + y 2 - 2 y + 2 z 2 = 2

Aí temos um termo com y 2 e com y , acho que temos que completar quadrados. Vamos lá:

x 2 + ( y 2 - 2 y ) + 2 z 2 = 2

x 2 + y - 1 2 + 2 z 2 = 2 + 1

Assim, ficamos com

x 2 + y - 1 2 + 2 z 2 = 3

Dividindo tudo por 3 pra ficar 1 do lado direito:

x 2 3 + y - 1 2 3 + z 2 3 2 = 1

E vóialá, temos um elipsoide com centro em ( 0 , 1,0 ) e semieixos 3 ,   3 ,   3 2

Passo 2

Vamos fazer os traços:

Traços:

  • Traço no plano x y   z = 0 :

    • x 2 3 + y - 1 2 3 + 0 2 3 2 = 1

    x 2 + y - 1 2 = 3

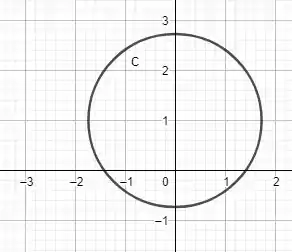
    Temos uma circunferência de centro em ( 0,1 ) e raio 3

  • Traço no plano x z   ( y = 0 ) :

    • x 2 3 + 0 - 1 2 3 + z 2 3 2 = 1

    x 2 3 + z 2 3 2 = 1 - 1 9 = 8 9

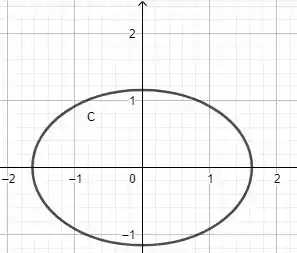
    E, agora, temos uma elipse de centro em ( 0,0 ) e semieixos 3 , 3 2 .

  • Traço no plano y z   ( x = 0 ) :

    • 0 2 3 + y - 1 2 3 + z 2 3 2 = 1

    y - 1 2 3 + z 2 3 2 = 1

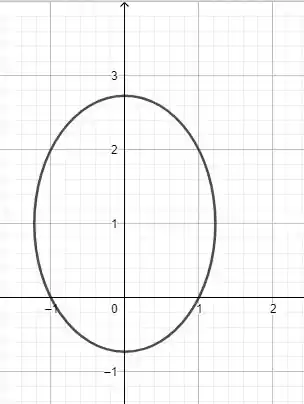
    Temos uma elipse de centro em ( 0,1 ) e semieixos 3 , 3 2 .

    Passo 4

    Vamos fazer agora interseções com planos paralelos aos eixos coordenados.

    Interseções:

  • Plano z = k

    • x 2 3 + y - 1 2 3 + k 2 3 2 = 1

    x 2 3 + y - 1 2 3 = 1 - k 2 3 2

    Se k > 3 2 , isso daí não vai estar definido, porque teremos dois termos ao quadrado se somando dando um valor negativo, o que é impossível. Mas, fora isso, para k ≠ 0 esse negócio aí pode é uma elipse no plano x y .

  • Plano y = k

    • x 2 3 + k - 1 2 3 + z 2 3 2 = 1

    x 2 3 + z 2 3 2 = 1 - k - 1 2 3

    De novo, temos que se k > 3 2 + 1 isso daí não vai estar definido, então não vai ter interseção. Mas, fora isso, para k ≠ 0 esse negócio aí pode é uma elipse no plano x z .

  • Plano x = k

k 2 3 + y - 1 2 3 + z 2 3 2 = 1

y - 1 2 3 + z 2 3 2 = 1 - k 2 3

Que são elipses no plano y z sempre que k < 3 .

Passo 3

Juntando tudo, o esboço fica:

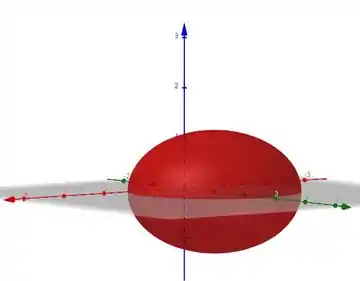
Passo 4

b )

Para encontrar a expressão do plano tangente à superfície S no ponto ( 1 , 1,1 ) , vamos seguir o passo a passo de plano tangente.

A primeira coisa e pegar a equação de S , jogar tudo pro lado esquerdo e chamar de F ( x , y , z ) :

F x , y , z = x 2 3 + y - 1 2 3 + z 2 3 2 - 1

Agora vamos calcular o gradiente de F :

∇ F = ( f x , f y , f z )

∇ F = 2 x 3 , 2 y - 1 3 , 4 z 3

Substituindo no ponto P 0 = ( 1,1 , 1 ) :

∇ F 1,1 , 1 = 2.1 3 , 2 1 - 1 3 , 4 3 = 2 3 , 0 , 4 3

E esse é o vetor normal ao plano.

Agora vamos substituir P 0 = ( 1,1 , 1 ) e o vetor normal ∇ F 1,1 , 1 = 2 3 , 0 , 4 3 na equação do plano tangente.

x - x 0 , y - y 0 , z - z 0 ⋅ n → = 0

x - 1 , y - 1 , z - 1 ⋅ 2 3 , 0 , 4 3 = 0

2 3 x - 1 + 0 y - 1 + 4 3 z - 1 = 0

x + 2 z = 3 2

Passo 5

c )

Agora, para encontrar a reta normal a superfície S no ponto ( 1 , 1,1 ) , também temos um passo a passo.

Acontece que o passo a passo é todo igual a esse que acabamos de fazer para o plano tangente (grazadeus, menos trabalho).

Mas agora, se pro plano tangente o vetor gradiente de F é um vetor normal, pra reta normal, ele vai ser o vetor que está na direção da reta normal.

Assim, substituindo o ponto P 0 = ( 1,1 , 1 ) e o vetor diretor ∇ F 1,1 , 1 = 2 3 , 0 , 4 3 na equação da reta normal, temos

r t = P 0 + n → t

r t = ( 1,1 , 1 ) + 2 3 , 0 , 4 3 t

Com t ∈ R .

Resposta

  1. A superfície S é:

  2. x + 2 z = 3 2
  3. r t = ( 1,1 , 1 ) + 2 3 , 0 , 4 3 t   , t ∈ R .

Exercícios de Livros Relacionados

Encontre uma equação (a) do plano tangente e (b) da reta normal à superfície dada no ponto especificado. x - z = 4a r c t g y z 1 + π ,1 ,1
Encontre uma equação (a) do plano tangente e (b) da reta normal à superfície dada no ponto especificado. 2 x - 2 2 + y - 1 2 + z - 3 2 = 10 3,3 , 5
Encontre uma equação (a) do plano tangente e (b) da reta normal à superfície dada no ponto especificado. y = x 2 - z 2 4,7 , 3
Determine as equações do plano tangente e da reta normal ao gráfico da função dada, no ponto dado. f x , y = 3 x 3 y - x ye m1 , - 1 , f 1 , - 1