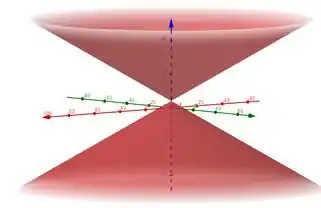
Obtenha uma equação cartesiana (livre de parâmetros) para a superfície cônica , cujo vértice é e cuja diretriz é a curva
Faça um esboço de .
Passo 1
Para que um ponto pertença a , deve existir um ponto de tal que . Então temos
Daí temos que e .
Então, .
Como o vértice não satisfaz essa equação, temos que incluí-lo multiplicado a equação por . Isso nos dá
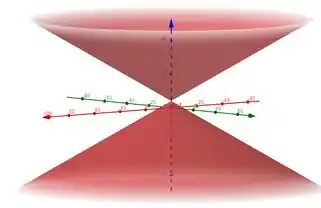
Resposta
Exercícios de Livros Relacionados
Obter uma equação da superfície gerada pela rotação de cada uma das curvas dadas em torno do eixo indicado. b )x 2 4 + y 2 16 = 1 ; z = 0 ; e i x om e n o r .
Obter uma equação da superfície gerada pela rotação de cada uma das curvas dadas em torno do eixo indicado. x 2 4 + y 2 16 = 1 ; z = 0 ; e i x om a i o r .
Obtenha, em cada caso, uma equação livre de parâmetros para a superfície gerada pela rotação da curva Γ em torno de O z ( Γ é descrita por equações paramétricas).(c) Γ : x = λ + 1 ,y = λ - 1 ,z = λ 2
Se as retas r e s são reversas, não ortogonais, a superfície gerada pela rotação de s em torno de r é uma que já estudamos. Identifique-a.
Completando os quadrados, identifique as superfícies de nível definidas por cada uma das formas quadráticas abaixo: 2 x 2 + y 2 - 4 x y - 4 y z