Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Superfícies

Ver Teoria
Exercício 912345678101112131415161718192021222324252627

Enunciado

No plano x O y considere a parábola P : y 2 + x - 4 y = 0 .

a) Determine o vértice e o foco de P .

b) Esboce P .

c) Escreva a equação da diretriz de P .

d) Escreve uma equação livre de parâmetros para a superfície no espaço obtida pela rotação da parábola

P :   y 2 + x - 4 y = 0 z = 0

Em torno do eixo O y .

Passo 1

a) Vamos completar os quadrados da equação de P :

y 2 - 4 y = - x

y 2 - 4 y + 4 = - x + 4

x - 4 = - ( y - 2 ) ²

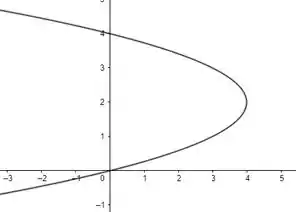
Pela equação, vemos que o vértice é V = ( 4 ,   2 ) .

p vale 1 4 e portanto F = 4 - 1 4 ,   2 = 15 4 ,   2 (lembrando que como o quadrado está em y , a parábola está de lado, então seu foco em y é o mesmo que seu vértice).

Passo 2

b) Com base no que sabemos da geometria dessa parábola (que ela está de lado) e sabendo o vértice e foco, seu esboço será assim

Passo 3

c) A diretriz l será paralela ao eixo y e vai ser dada pelo vértice em x somado a p , ou seja:

l : x = 4 + 1 4  

l : x = 17 4

Passo 4

d) A superfície que estamos procurando é a união das circunferências que têm centro no eixo O y . Para que um ponto genérico X = ( x ,   y ,   z ) esteja em uma dessas circunferências, ela deve ter centro C = ( 0 ,   y ,   0 ) e conter o ponto Q = u ,   y ,   0 ∈ P , seja u o equivalente a x na equação de P dada no enunciado.

Isso só vai ocorrer se C X → = C Q → . Logo:

( x ,   0 ,   z ) = | ( u ,   0 ,   0 ) |

x 2 + z 2 = u ²

Sabendo que u equivale a x e isolando x na equação de P , temos que u = - y 2 + 4 y :

x 2 + z 2 = ( - y 2 + 4 y ) ²

x 2 + z 2 = 16 y 2 - 8 y 2 + y 4

Resposta

a) V = ( 4 ,   2 ) F = 15 4 ,   2

b)

c) l : x = 17 4

d) x 2 + z 2 = 16 y 2 - 8 y 2 + y 4

Exercícios de Livros Relacionados

Obter uma equação da superfície gerada pela rotação de cada uma das curvas dadas em torno do eixo indicado. b )x 2 4 + y 2 16 = 1 ; z = 0 ; e i x om e n o r .
Obter uma equação da superfície gerada pela rotação de cada uma das curvas dadas em torno do eixo indicado. x 2 4 + y 2 16 = 1 ; z = 0 ; e i x om a i o r .
Obtenha, em cada caso, uma equação livre de parâmetros para a superfície gerada pela rotação da curva Γ em torno de O z ( Γ é descrita por equações paramétricas).(c) Γ : x = λ + 1 ,y = λ - 1 ,z = λ 2
Se as retas r e s são reversas, não ortogonais, a superfície gerada pela rotação de s em torno de r é uma que já estudamos. Identifique-a.
Completando os quadrados, identifique as superfícies de nível definidas por cada uma das formas quadráticas abaixo: 2 x 2 + y 2 - 4 x y - 4 y z