UTFPR – Pato Branco – Física 1 – SUB – 2022.2 – 2
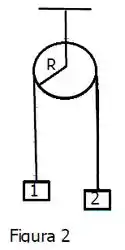
Dois blocos com massas e estão conectados um ao outro por meio de uma corda com massa desprezível que passa por uma polia de massa com formato de um disco rígido de raio (Figura 2). Encontre a aceleração dos blocos e as tensões na corda. (Assuma que não há deslizamento entre a corda e a polia.)
Passo 1
Fala, galera! Vamos responder essa questão.
O enunciado nos deu duas massas conectadas por uma corda e uma polia de massa e pediu pra gente encontrar a aceleração dos blocos e as tensões nas corda. Pra isso, nós vamos precisar dar uma olhadinha nos diagramas de corpo livre de cada elemento:
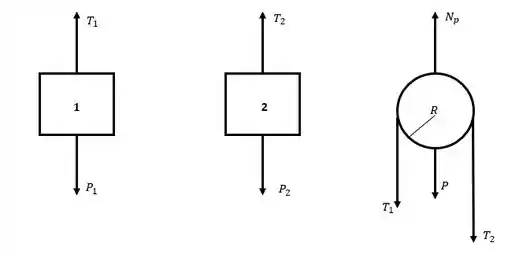
E então, nós vamos aplicar a segunda lei de Newton (), fazendo o somatório de forças em cada um dos elementos.
Vamos lá!
Passo 2
Para o bloco , nós temos:
Como , ficamos com:
Para o bloco 2 é bem parecido. Nossa equação fica:
Temos incógnitas para duas equações, precisamos trazer a polia para os cálculos. Teremos que trabalhar com rotação, visto que a polia exerce um movimento de rotação. O que vem na sua cabeça? Momento de inércia!
Então, para a polia temos:
Simplificando:
Passo 3
Agora já temos equações para incógnitas:
Substituindo e na terceira equação, temos:
Reagrupando:
Vamos isolar a acelaração :
O enunciado nos deu , e . Substituindo na nossa equação:
O sinal negativo significa que ela está apontando pra baixo.
Passo 4
Agora só falta a gente encontrar as tensões nas cordas. Usando a primeira equação:
Substituindo os valores que encontramos:
E para a tensão :
E encerramos o exercício. Valeu, galera! 😉