As posições de um objeto em movimento bidimensional são dadas pelo vetor posição: , onde todas as quantidades estão no sistema internacional de unidades. Qual é o ângulo que o vetor velocidade faz com o eixo no instante após iniciado o movimento?
(A)
(B)
(C)
(D)
(E)
Passo 1
A posição da partícula varia em função do tempo de acordo com o vetor posição :
Mas não estamos interessados diretamente no vetor posição e sim no vetor velocidade .
Mas qual o vetor velocidade ?
Bom, lembra que a velocidade é a variação da posição?
Na verdade, a velocidade média...
Mas e se quisermos uma velocidade precisa em um instante de tempo (por exemplo: ?
A ideia é calcular a velocidade média com um intervalo de tempo tão pequeno que ele tende a zero, ou seja, calculando assim a velocidade instantânea.
Isso que acabamos de dizer é o conceito de Derivada, ou seja, a velocidade é a derivada da posição:
Ou ainda na forma vetorial:
Então, vamos derivar esse vetor posição para achar o vetor que queremos .
Passo 2
Para derivar um vetor, basta derivar cada uma de suas componentes:
Passo 3
Agora, podemos encontrar qual pe o vetor velocidade no instante .
Mas, muita atenção!
O enunciado deixou claro que o vetor estava nas unidades do Sistema Internacional, ou seja, o tempo está em segundos .
Logo o instante de tempo deve entrar na expressão como :
Passo 4
Para achar o ângulo que esse vetor faz com a horizontal, podemos usar uma relação entre suas componentes:
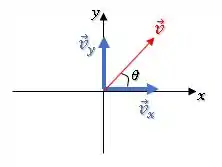
Se deslocarmos , podemos ver que temos um triâgulo retângulo.
Então, podemos relacionar as duas componentes com o ângulo a partir de:
Qual o ângulo que tem tangente igual a ?
Isso mesmo:
Então, o vetor velocidade no instante faz com a horizontal.
Resposta
Letra (D)