Uma partícula tem uma aceleração constante . No tempo , a velocidade é zero e o vetor posição é . Encontre os vetores velocidade e posição em função do tempo . Encontre a equação da trajetória (de em função de ) da partícula no plano e esboce a trajetória.
Passo 1
O problema nos fornece a equação da aceleração de um partícula e nos pede os vetores velocidade e posição em função do tempo.
Como a variação da velocidade é a integral da aceleração e o vetor deslocamento é a integral da velocidade. Precisamos apenas integrar a equação da aceleração. Então vamos lá.
Passo 2
Primeiro vamos encontrar a equação da velocidade, integrando a aceleração
Substituindo os valores de , e o de que o enunciado diz ser zero.
Passo 3
Para achar o vetor posição devemos integrar a velocidade
Vamos substituir os valores que acabamos de encontrar e o valor de
Passo 4
Para acharmos a equação da trajetória temos que sumir com o tempo e deixar a equação de forma que fique em função de
Pela equação da posição que acabamos de encontrar tempos que a posição e a posição .
Se isolarmos o tempo na equação de , temos
Podemos substituir isso na equação de e assim achamos a relação entre e
Isolando para acharmos a equação da trajetória
A trajetória será uma reta no plano
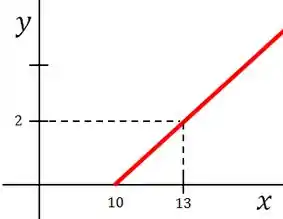
Resposta