UFABC – Fenômenos Mecânicos – Lista 3 – Questão 02
A posição de um elétron que se move ao longo do eixo é dada por , onde está em segundos. A que distância da origem se encontra o elétron quando para momentaneamente?
Passo 1
Oi! Essa questão parece complicada, mas vou ajudar você!
O problema nos deu uma função que representa a posição e um elétron em um instante de tempo . E ele nos perguntou a que distância da origem ele se encontra quando para momentaneamente.
Em outras palavras, o que ele pergunta é onde (em que posição) a velocidade é zero
Pessoal, esse é um caso que precisamos usar derivada, porque a velocidade é a derivada da posição. A questão dá a função posição em relação ao tempo, para descobrir a velocidade instantânea da partícula devemos derivar.
Depois de encontrar a derivada, vamos igualar o resultado a zero, pois queremos saber em que instante de tempo isso ocorre.
E por fim, com o instante de tempo, vamos voltar para a equação para a posição e substituir. Assim saberemos a posição na qual a velocidade é zero.
Beleza? Mas relaxa, vou fazer passo a passo com você!
Passo 2
A equação horária da posição desse elétron é:
E agora vamos derivar em relação ao tempo, pra achar a velocidade instantânea:
Mas como essa função é um produto (de por uma exponencial), vamos usar a regra do produto:
Derivando...
E juntando os termos semelhantes
Taí temos a função que representa a velocidade!
Nossa missão agora é ver onde ela é zero!
Passo 3
Devemos fazer e descobrir para qual valor de a equação é satisfeita.
Para isso um dos fatores deve ser igual a zero para algum valor de .
- é diferente de zero para todo valor de e
- é igual a zero para .
Olha só um gráfico da posição pelo tempo:
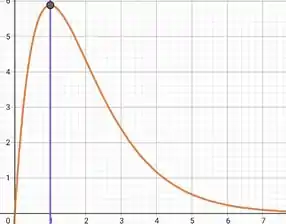
Verificamos que no instante temos um pico no gráfico, ali onde a inclinação da reta tangente (que representa a velocidade) é horizontal, ou seja, velocidade igual a zero mesmo!
Passo 4
Show de bola! Agora que temos o instante em que o elétron para momentaneamente podemos achar a distância em relação a origem substituído o valor de na equação da posição:
Tranquilo? Espero ter ajudado!
Vamos para a próxima!