A posição de uma partícula em metros é descrita pelo vetor posição .
Considere as afirmativas abaixo:
() A partícula passa pela origem do sistema de coordenadas.
() A tangente do ângulo entre o vetor velocidade e o eixo em é .
() O movimento da partícula não é acelerado.
Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Passo 1
Temos uma expressão para a posição da partícula em função do tempo. O único detalhe é que essa posição está sendo dada na forma de um vetor em e .
Vamos analisar cada afirmativa.
Passo 2
() A partícula passa pela origem do sistema de coordenadas.
Para que a partícula passe pela origem, basta que em algum instante de tempo a sua posição seja .
Então, vamos checar se isso acontece tanto em quanto em num mesmo instante.
Primeiro, vamos ver em quais instantes a partícula tem sua coordenada igual a zero:
Opaaa... achamos que a coordenada zera apenas em um instante de tempo negativo.
Como o tempo começa em , esse instante não existe.
A afirmativa () está incorreta.
Passo 3
() A tangente do ângulo entre o vetor velocidade e o eixo em é .
Vamos por partes.
Quem é o vetor velocidade?
Bom, a velocidade é a variação da posição, ou seja, sua derivada:
Agora, vamos descobrir o vetor velocidade no instante :
Agora, vamos calcular a tangente do ângulo que o vetor faz com a horizontal:
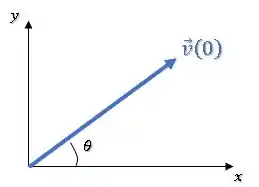
Para isso, basta usar as componentes em e em :
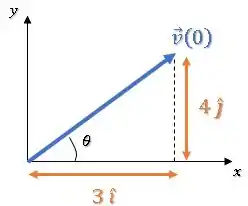
A afirmativa () está correta.
Passo 4
() O movimento da partícula não é acelerado.
Olhando para o vetor velocidade:
Podemos ver que ele varia, pois o termo da componente em tem um que vai alterar conforme o tempo.
Mas se quisermos ver explicitamente o vetor aceleração, basta derivar novamente:
Então, podemos ver que para todo instante de tempo após , há um vetor aceleração diferente de zero.
Assim, temos um movimento acelerado.
A afirmativa () está incorreta.
Temos apenas como correta, então, ficamos com a letra (b).
Resposta
Letra (b)