UnB - Física 1 - Listas - Lista 2 Movimento em Uma Dimensão - Questão 1a
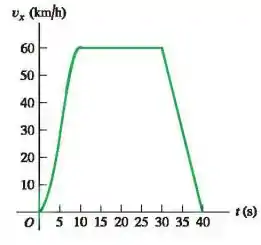
A figura abaixo mostra a velocidade de um carro movido à energia solar como uma função do tempo. O motorista acelera a partir de uma placa de pare, dirige por com velocidade constante de e começa a frear até o repouso após deixar a placa de pare.
Calcule a aceleração média durante os seguintes intervalos:
(i) ;
(ii) ;
(iii) ;
(iv) .
Passo 1
Fala aí, beleza?? Vamos para mais uma questãozinha! Bom gente a partir do gráfico vamos identificar qual é o tipo de movimento, sendo assim:
De a : Movimento acelerado, onde a aceleração não é constante!
De a : Movimento Uniforme, onde a aceleração é nula.
De a : Movimento Uniformemente Variado, onde a desaceleração é constante.
Após a interpretação do gráfico vamos calcular a aceleração média para cada intervalo.
Atenção!
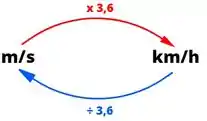
Observem que no temos a velocidade em enquanto que no temos o tempo em . Dessa forma é indispensável sempre transformar a velocidade para antes de efetuar qualquer cálculo para a aceleração.
Para o intervalo (i) , temos:
A velocidade em :
A velocidade em :
Sendo assim,
Passo 2
Já para o intervalo (ii) , onde a desaceleração é constante podemos calcular a aceleração média pela fórmula:
Entretanto antes precisamos transformar os valores das velocidades de para . Para fazer essa transformação basta dividir o valor de por 3,6. Sendo assim
Portanto,
Passo 3
Bom pessoal para o intervalo (iii) , temos que a velocidade permanece constante e igual a . Podemos concluir então que se não há variação da velocidade é porque a aceleração é nula.
Passo 4
E por fim para o intervalo (iv) , a aceleração média vai ser a média das diferentes acelerações que o veículo teve durante todo o percurso.
Tudo tranquilo? Show! Bora fazer mais!