Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Potencial e Trabalho

Ver Teoria
Exercício 11123456789101213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758

Enunciado

Forças Elétricas, Energia Potencial e Densidade de Energia

Quatro partículas puntiformes com cargas e massas iguais estão disposta nos vértices de um quadrado de lado a .

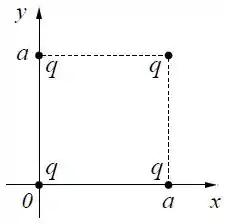
  1. Qual é o vetor força elétricas sobre a carga na posição x = a ,   y = a ?
  2. Que trabalho foi realizado para trazer a última carga para o seu lugar desde o infinito?
  3. Qual é a energia cinética de cada carga no infinito se forem retirados simultaneamente todos os vínculos que prendem as cargas em seus lugares?

Passo 1

  1. Qual é o vetor força elétricas sobre a carga na posição x = a ,   y = a ?

    2. De acordo com a lei de Coulomb, a força entre as cargas é dada por:

    F → = q 1 q 2 4 π ϵ 0 r 2 r ^

    Assim, a força resultante vai ser a soma das forças. Só precisamos calcular cada uma separada e somar no final, sem mistério, né?

    1. Carga em 0 , a :

      2. F 1 → = q 2 4 π ϵ 0 a 2 i ^

    2. Carga em a , 0 :

      3. F 2 → = q 2 4 π ϵ 0 a 2 j ^

    3. Carga em a , a :

    Nesse caso, a distância entre as cargas é r = 2 a

    F 3 → = q 2 4 π ϵ 0 2 a 2 2 2 i ^ + 2 2 j ^

    F 3 → = q 2 4 π ϵ 0 a 2 2 4 i ^ + 2 4 j ^

    Como eu disse antes, agora só temos que somar esses caras:

    F → = q 2 4 π ϵ 0 a 2 1 + 2 4 i ^ + 1 + 2 4 j ^

    F → = q 2 4 π ϵ 0 a 2 4 + 2 4 i ^ + 4 + 2 4 j ^

    F → = 4 + 2 q 2 16 π ϵ 0 a 2   i ^ + j ^

    Passo 2

  2. Que trabalho foi realizado para trazer a última carga para o seu lugar desde o infinito?

    3. O trabalho realizado para trazer a última carga para o seu lugar desde o infinito será:

    W = q V 3

    Onde V 3 é o potencial elétrico das outras três cargas no ponto onde a última vai ser colocada.

    O potencial elétrico é dado por:

    V r = q 4 π ϵ 0 r

    Duas cargas estão a uma distância r = a da última carga, e apenas uma carga (a que vai ser em diagonal) está a uma distância r = 2 a da última carga.

    Logo:

    V 3 = q 4 π ϵ 0 a + q 4 π ϵ 0 a + q 4 π ϵ 0 a 2

    V 3 = q 4 π ϵ 0 a   2 + 2 2

    Agora, substituindo na fórmula do trabalho:

    W = q 2 4 π ϵ 0 a   2 + 2 2

    Passo 3

  3. Qual é a energia cinética de cada carga no infinito se forem retirados simultaneamente todos os vínculos que prendem as cargas em seus lugares?

Bom, como todas as cargas são iguais e o sistema apresenta simetria, faz sentido que todas as cargas possuam a mesma quantidade de energia cinética? (Sim, vai por mim)

Assim, qual a parada aqui?

A parada aqui é, a partir da conservação de energia, calcular a energia cinética total do sistema e dividir por quatro. Assim vamos encontrar a energia cinética de cada carga se elas forem retiradas simultaneamente. Foi numa boa?

Então vamos lá!

Nós temos 6 pares de cargas, em 4 dos pares, as cargas distam uma da outra de a , já nos outros dois pares, as cargas distam uma da outra de a 2 , beleza?

A energia potencial elétrica para cada par de carga é dada por:

U r = q 1 q 2 4 π ϵ 0 r

Lembrando que a energia total deve ser dividida por 4:

E c i n = 1 4   4 × q 2 4 π ϵ 0 a + 2 × q 2 4 π ϵ 0 a 2

E c i n = q 2 16 π ϵ 0 a   4 + 2

E c i n = q 2 4 π ϵ 0 a   1 + 2 4

Resposta

  1. F → = 4 + 2 q 2 16 π ϵ 0 a 2   i ^ + j ^

  2. W = q 2 4 π ϵ 0 a   2 + 2 2

E c i n = q 2 4 π ϵ 0 a   1 + 2 4

Exercícios de Livros Relacionados

Uma placa não condutora infinita possui uma densidade superficial de cargas σ = + 5,80p C / m 2 . (a) Qual é o trabalho realizado pelo campo elétrico produzido pela placa se uma partícula de carga q =
Uma esfera não condutora tem raio R = 2,31c m e uma carga uniformemente distribuída q = + 3,50f C . Tome o potencial elétrico no centro da esfera como V 0 = 0 . Determine o valor de V para uma distânc
A abaixo mostra um gráfico da componente x do campo elétrico em função de x em uma certa região do espaço. A escala do eixo vertical é definida por E X S = 20,0 N/C. As componentes y e z do campo elét
Duas placas paralelas condutoras de grande extensão estão separadas por uma distância de 12 cm e possuem densidades superficiais de cargas de mesmo valor absoluto e sinais opostos nas faces internas.
Energia do núcleo. Qual é a energia necessária para montar um nũcleo atômico contendo três prótons (tal como Be), se o modelarmos como um triângulo equilátero de lado 2 ⋅ 10 - 15 m . com próton em cad