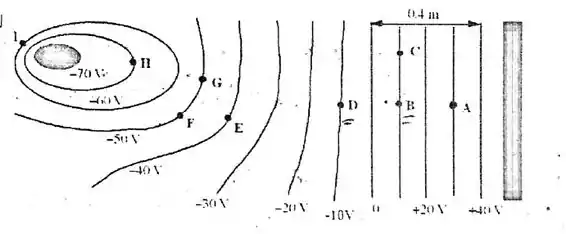
O desenho abaixo mostra as seções transversais de superfícies equipotenciais entre dois condutores carregados que são mostrados em preto. Vários pontos nas superfícies equipotenciais próximos dos condutores estão marcados A, B, C, ..., I. Uma carga pontual ganha de energia cinética quando se move do ponto E para o ponto A. Determine a magnitude, o tipo da carga e quanto trabalho é necessário para movê-la do ponto B para o ponto D.
a) , negativa, e
b) , negativa e
c) , positiva e
d) , positiva e
e) , negativa e
Passo 1
Temos que o trabalho se relaciona com a variação de energia cinética por
Por outro lado, esse trabalho se relaciona com a variação de energia potencial elétrica
Pela figura acima temos que
Então:
Ou seja, a carga é negativa!
Passo 2
Para mover do para o , temos que usar a mesma fórmula:
Já sabemos . Temos que
Repara que agora é negativo! Isso vai ter influência no sinal do nosso trabalho.
Resposta
(e)