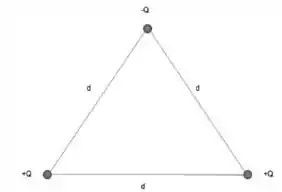
Qual a quantidade de energia necessária para construir o arranjo da figura abaixo trazendo as cargas do infinito?

1. .
2. .
3. .
4. .
5. .

Vamos começar a resolver essa questão numerando cada uma das partículas, como fizemos na figura abaixo. É legal fazer isso também para o caso que existem mais do que três cargas e que pode aparecer para você, pois facilita na hora que você for contabilizar quais pares de cargas contribuirão para a energia do sistema.

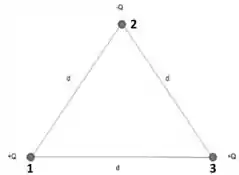
É importante lembrar que só contamos um par uma única vez para calcularmos a energia eletrostática. No caso desta questão, temos que fazer as seguintes interações: 1 com 2, 1 com 3 e 2 com 3. Repara que a interação de 2 com 1 já foi contada uma vez, assim como a interação 3 com 1 e assim por diante.

Colocando em termos da energia de interação entre as cargas e , teremos:

Simplificando essa expressão, obtermos que a energia total do sistema é

Então, não tem erro, se você tem várias cargas e tem que calcular a energia total de todas elas, coloque números nas cargas e contabilize a energia de todos os pares de cargas, tomando cuidado de contar a energia de um par uma única vez, beleza??

Depois, só partir para o abraço...